Will This Be on the Test? (October 2023)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test. Here is this month’s question:


How can you approach this question in a way that makes sense to you? What conceptual understandings or visual tools can you bring to bear? What mathematical concepts do students really need to be able to tackle this problem? How might your real-world experience help you reason about this?
My first instinct with a question like this is to wonder why the goat is tied to a fence post when the whole pasture is fenced in! Maybe you are wondering something similar. Or, since goats are notorious for eating anything and everything, I wonder whether the goat wouldn’t just chew through the rope and thereby get access to the whole pasture. While these musings aren’t really useful in choosing the correct answer, if a student brought them up in class, I would celebrate them. Math is a tool for reasoning about the real world, and if we want students to use math in their lives, they’ll need to be able to do more than pick a correct answer on a standardized test. Students should be encouraged to identify situations in which math will be helpful to them so that they can use appropriate tools strategically (MP.5)* and use math effectively to model real situations (MP.4)*. On a test, we must accept the scenarios as they are given, but having developed the habit of questioning the given information will still help students think creatively and flexibly in test situations.
Here are some possible approaches to this task beyond what the test-makers might have had in mind:
1. Draw a picture to make sense of the story. With a question about a geometric situation, it’s hard to imagine that drawing a picture wouldn’t help. There is a shape present in the story that isn’t named. By imagining the shape created when the goat stretches out its rope to the full length and sketching a picture, a student can visually access a lot more information than was immediately apparent from reading the words in the task. If the goat could roam to the end of its rope in all directions, it would have a circle to graze in, but it is also limited by the fence. What do you notice from this sketch? What do you wonder? What ideas does it inspire about strategies?
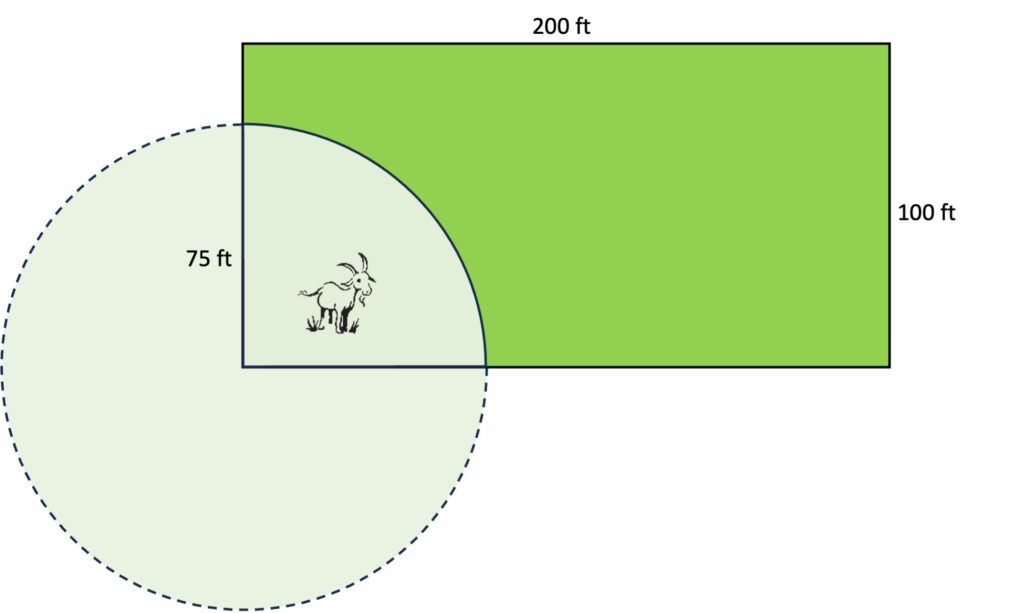
2. Draw roughly to scale and estimate. Check with a calculator. The sketch above is roughly to scale. The 200 foot dimension is about twice as long as the 100 foot dimension, and the 75 foot rope is about ¾ of the 100 foot dimension. With this picture, a student might be able to estimate the area available to the goat. For example, they could start by estimating that the area available to the goat is less than half the area of the whole pasture:
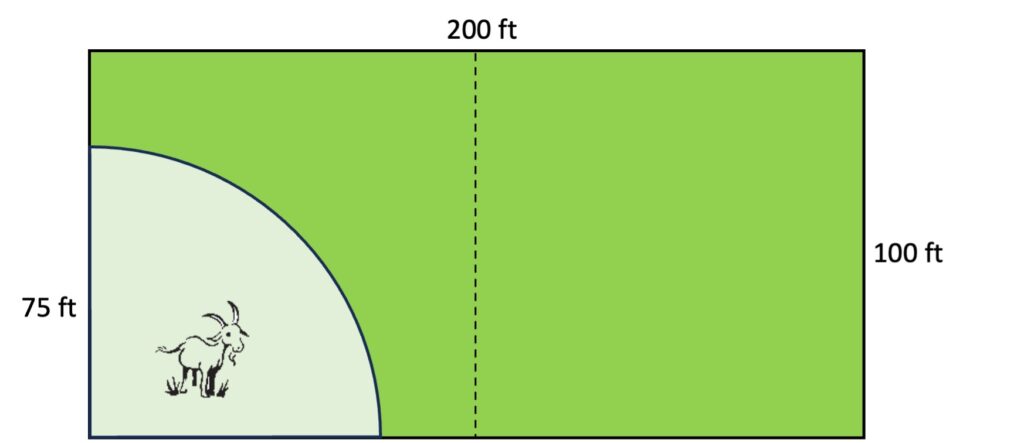
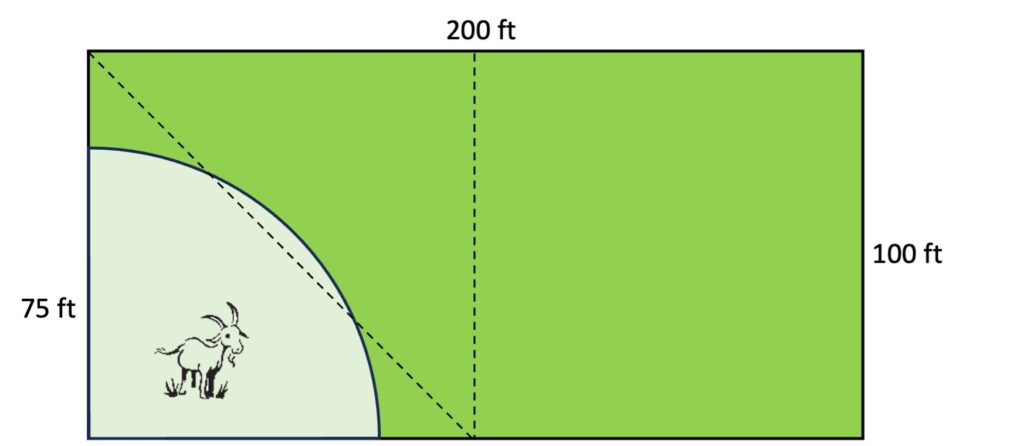
Cutting the left half with a diagonal shows that the area available to the goat appears to be less than half of a half of the whole pasture, or less than one-fourth of the whole pasture. (Or on a rougher sketch, it might be hard to tell whether it’s a little more or a little less than one-fourth of the pasture, but saying it’s close to one-fourth is also a good estimate. Regardless, the skill of partitioning shapes into fractions in different ways comes in very handy here!)
A student who doesn’t recognize the shape of the area available to the goat or who doesn’t know how to find its area, might still be able to find the area of the whole pasture and figure out one-fourth of that. Once they have an estimate, they could use a calculator to calculate the values of the different answer choices and see which one or ones come out close to their estimate.
3. Tell a story of how you would find the area. One thing that is really challenging about a question like this is that the correct answer choice may not match how the student reasoned about the task. There are many correct expressions that could be used to find the area available to the goat, but only one of those is listed in the answer choices. However, if students practice connecting stories to expressions and expressions to stories, they will not be fazed by not seeing their own reasoning reflected in the answer choices and may be able to recognize the “correct” answer. For example, if the student’s story is, “First I would find the area of a whole circle whose radius is 75 feet, and then I would divide that area by 4 to get the quarter-circle in my picture,” the student’s expression might be (752 ✕ 𝜋) ÷ 4. Even though that expression is not among the answer choices, the student could look for an expression with similar elements and tell the story of that expression to see if it also would work to find the desired area. (For more about “choose the correct expression” type problems, see the January 2022 installment of Will This Be on the Test.)
4. Consider what is relevant. Starting once again with the sketch, a student might realize that the area available to the goat would be the same even if the pasture had larger dimensions because the rope keeps the goat from reaching the other sides. For example, the pasture could be 500 ft by 500 ft and it wouldn’t change the area available to the goat. This means that the dimensions of the pasture are not necessary to finding the area the goat can graze on. Therefore, any expression that uses those numbers must not be the correct one! Which answer choices seem reasonable now?
Drawing pictures is a powerful way to make sense of problems. I used to try to hold everything in my head and use as little paper as possible, as if there was some virtue in not writing things down. It took seeing other people’s pictures to open my eyes to what I could gain from drawing my own. Now I reach for pencil and paper to draw out math tasks almost instinctually – because seeing my own thinking with my eyes reduces strain on my working memory, opens up new ways of perceiving, and makes my thinking more efficient.
*MP refers to the 8 CCR Standards for Mathematical Practice. Learn more at https://www.thecorestandards.org/Math/Practice/

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
