Blog

Will This Be on the Test? (Jan 2022)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a high school equivalency test. For this first installment of 2022, I think it’s time to finally tackle a type of question that I’ve been avoiding. Here it is:

In my own reflections, I realized that when faced with problems like this in the past, I have departed from my priorities of teaching conceptually and resorted instead to lessons on test-taking strategy. While it is important that students have some idea of what they are walking into when they take the test, I hate devoting classroom time to something that will only ever serve them in a test situation and be of no use to them in their lives.

I have been avoiding bringing this type of question into this column because, in my opinion, it is not a fair way to assess a student’s understanding or ability to use math to answer real world questions. One test prep book I pulled off my shelf implied that this type of question is easier for students because they do not have to actually solve a word problem, they only have to choose the “proper” way to set it up. However, in the real world, there is no one right way to determine Alicia’s earnings for the week, and students who have learned to think flexibly and play to their strengths may come up with a different approach than the “right” answer in the set of multiple-choice options.

Instead of exploring multiple paths to the solution, this month let’s talk about how we can prepare students to apply their math successfully on problems like these without sacrificing our precious teaching time to something that feels like it is only test prep. What can we be teaching students that advances their numeracy and confidence and at the same time prepares them to tackle questions like the one above?

The key concept here is that expressions like the ones in the answer choices are ways of recording thinking. Because not everyone will think about the calculations the same way, people will write different expressions to record their thinking.

For example, a student might reason about Alicia’s earnings this way:

---

First, I’ll figure out her earnings from her hourly wage – that’s $18.50 x 35 since she worked 35 hours at $18.50 an hour.

Then I’ll figure out her commission on the dishwasher – that’s 1/5 of $600 since 20% is the same as 1/5.

Then I’ll figure out her commission on one of the microwaves. That’s 1/5 of $400.

Since she sold two microwaves, I’ll add that last number on again for the second microwave.

---

How does that reasoning translate into an expression? It translates in chunks, just like the reasoning itself. (Using color to highlight how the parts of the expression correspond to the verbal reasoning can help connect the symbolic notation to the thinking it represents. Students who cannot distinguish colors may choose to use different ways of underlining or circling chunks instead.)

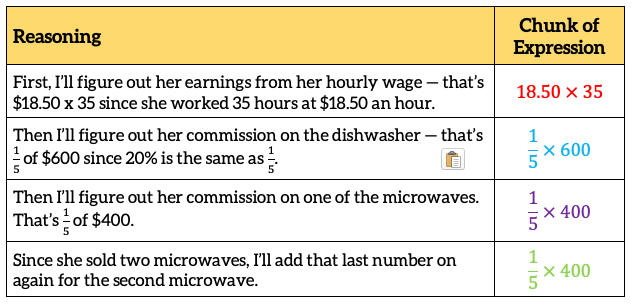
All together, the expression looks like this:

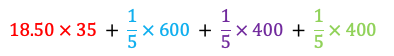
Or like this, if the student chooses to use parentheses to be extra clear about how the thinking is chunked (a practice that is not always necessary, but can be helpful):

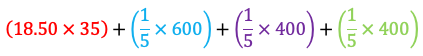
In this way, the student has used mathematical notation to tell a story of their thinking. This is an important skill for answering test questions like the one at the top of this column, but it also is helping the student focus and communicate their reasoning and preparing them for further work with expressions and equations as they move to higher levels.

But there is a big problem here – the perfectly good expression the student came up with is not among the answer choices. Because this can happen (and often does), students need more skills than being able to record their thinking with symbols to be able to answer the question. There is one more skill and one more understanding students need to be able to navigate “which expression?” type problems:

1. They need to understand that different expressions can have the same value (or be equivalent).
2. They need to be able to read and interpret expressions as telling stories of a way of thinking. 

Both of these things can be taught through engaging, conceptual, collaborative work. For example, in your class, you might ask your students to each write their own expressions for Alicia’s earnings. Another student might reason this way:

---

First, I’ll figure out the total sales she made – that’s $600 for the dishwasher and 2 × $400 for the two microwaves.

Then, I’ll figure out 20% of her total sales by multiplying the total sales by 0.2.

I’ll figure out how much she earned from her hourly wage by multiplying the hours by the wage, so that’s 35 × $18.50.

---

Translating this reasoning to an expression might look something like this. The student might start by writing their first step as:

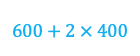
Then continue by multiplying that by 0.2 to get:

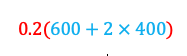
And finally add on the result of the third calculation to get:

If you have ten students in your class, you may well now have a collection of ten different expressions that represent Alicia’s earnings for the week. Asking students to share their thinking and their expressions sets up an important aha moment. While there is only one correct answer to the amount Alicia earned, there are many ways to get there and different mathematical notation can be used to represent the same end value. In other words, different expressions can be equivalent. (This is a key principle underlying what many people think of as “doing algebra.”)

The final piece, reading an expression and figuring out the story it tells, can be explored in this same lesson. Have your students trade expressions and try to figure out each other’s thinking. This takes practice, but this cycle of writing expressions to record thinking, recognizing that expressions can be equivalent, and reading expressions with the goal of understanding the story they tell can be repeated many times in different contexts, at different levels, and in different domains. For example, students may come up with many different ways of expressing the perimeter of a rectangle and practice connecting the different formulas that arise to the different ways of thinking about perimeter. (To see a lesson that explores perimeter in this way and connects to using variables in expressions at early levels, see Unit 1, Lesson 4 – Understanding Perimeter with Formulas in the Curriculum for Adults Learning Math (CALM) at calm.terc.edu.)

Wrapping up a lesson (or several) like this with test-like questions like the one at the top of this column can now be a chance for students to practice reading expressions and understanding the stories they tell. The incorrect answers also tell stories, but they are incorrect stories. For example, a student might read answer choice (C) 35(18.50) + 0.2(600) + 0.2(400) and realize that it is telling the story of a week where Alicia sold the dishwasher but only sold one microwave. This could be a great extension activity – trying to figure out what story each answer choice tells and whether that story makes sense. For example, answer choice (E) 35(18.50 + 600 + 2 x 400) adds together Alicia’s hourly rate and the value of the items she sold and then multiplies that whole thing by the number of hours she worked. This story says that Alicia makes $18.50 plus the value of all the items she sells every hour that she works. This does not make sense at all!

A couple final thoughts about these choose-the-right-expression type problems:

These are not easy problems. Unless a student is lucky enough to think about the situation in exactly the same way the person who wrote the problem did, they will not find their expression among the answer choices. This can cause a lot of anxiety in the moment of taking the test. Students need to be secure in their understanding that there are multiple possible correct expressions so that they do not jump to the conclusion that their thinking is incorrect just because they don’t see their answer in the answer choices. Be careful not to pass on to your students the message that these are easy problems because you only have to find the expression and you don’t have to evaluate it. These problems take time because you have to look closely at each answer choice. Just because it is a multiple-choice question doesn’t mean it is quick and easy.

Finally, there is one test-taking strategy that can make a difference on a question like this. I would not teach this in place of the rigorous learning described above, but it is valuable for students to have. Students can circumvent the whole issue of figuring out what each expression means by answering the question themselves with a number (Alicia’s actual earnings) and then evaluating each expression to find which one gives the correct answer. This is not necessarily faster, but it is pretty reliable. It is also a strategy that is not useful after test day, as opposed to the ability to write and read expressions which is crucial for moving forward in algebra and beyond.

For an excellent activity and collection of related resources that build the skills and understandings discussed here, check out The Border Problem at CollectEdNY.

---