Will This Be on the Test? (Apr 2022)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a high school equivalency test. Are the flowers blooming where you are? Here is a spring challenge for you:


Pause to reflect. What skills and understandings are needed for this problem? How many approaches can you think of that might be accessible to students at a range of levels?
You may be thinking that this is the type of problem your students would turn and flee from – and sometimes running away (figuratively) and devoting their energy to more accessible problems is the best approach. We and our students should always keep students’ larger goals in mind. Regardless of whether students are planning to continue to further education or to employment that requires a high school equivalency, it is unlikely that they need to get every single problem right on the test.
However, this month let’s look at how this problem can be accessible. In my opinion, this falls into the not-as-scary-as-it-looks category.
Step one in making this kind of problem accessible is learning not to panic when we see letters and symbols. Test questions with equations or inequalities in them should not be a cause for panic for any student. This is not to say that students should be able to easily solve any equation, but they should be able to calmly decide whether to take on a test question. (This is a skill worth practicing – I’ve handed students practice tests cut apart into individual questions and had them sort them into yes, no, and maybe piles. This had an impressive effect on their confidence heading into the test, knowing they had the power to choose or refuse each question.)

Despite looking intimidating, though, I think this question could go in the maybe or yes pile for many students. What it is really about is Mathematical Practice 2 – reason abstractly and quantitatively. How I read this practice is that it is about understanding relationships well enough to strip away the context and represent them symbolically, but still staying connected to the context when reasoning about the relationships.
What makes this problem look scary is the inequality, but that is actually showing that the work of decontextualizing has been done for the student. A student who has practiced decontextualizing and contextualizing will feel comfortable with the idea that letters can stand for unknown numbers or even for numbers that can change. This practice can happen at any level because any student who is reasoning mathematically is reasoning about relationships. For example, beginning students can reason abstractly about the perimeter of rectangles and represent their thinking symbolically. To see a lesson that explores perimeter in this way and connects to using variables in expressions at early levels, see Unit 1, Lesson 4 – Understanding Perimeter with Formulas in the Curriculum for Adults Learning Math (CALM) at calm.terc.edu.
Go back and read the problem again. Does the student need to be able to write an inequality? Or solve one? Or graph one? Or even read one? In fact, this question is really asking which of the answer choices represents a number of bulbs Mark can buy without spending $60 or more. There is the intimidating extra factor of the answer choices being presented as ordered pairs, but the question does tell us what x and y represent. A student who can contextualize as well as decontextualize may be able to read the problem this way:

Doesn’t that look friendlier?
Now that we’ve done the admittedly nontrivial work of making sense of the problem, here are a few ways a student might persevere in solving it.
1. Remember the context. This question can be answered by checking all the answer choices; however, it may save some time to put a little thought into which answer choices are more likely to work. Mark is trying to spend under $60, so a student might look for an answer choice that has fewer of the more expensive large bulbs without having a lot of the less expensive small bulbs. A quick scan will show that answer choice b (4 large bulbs and 6 small bulbs) is not worth checking out because answer choice a (4 large bulbs and 5 small bulbs) has the same number of large bulbs but fewer small bulbs, so it must be less money. Which do you think looks like the cheapest option?
2. Write out all the possibilities. A question like this can be read as a set of yes or no questions instead of multiple choice. For each answer choice, calculate the cost and decide whether Mark can make that purchase. For example:
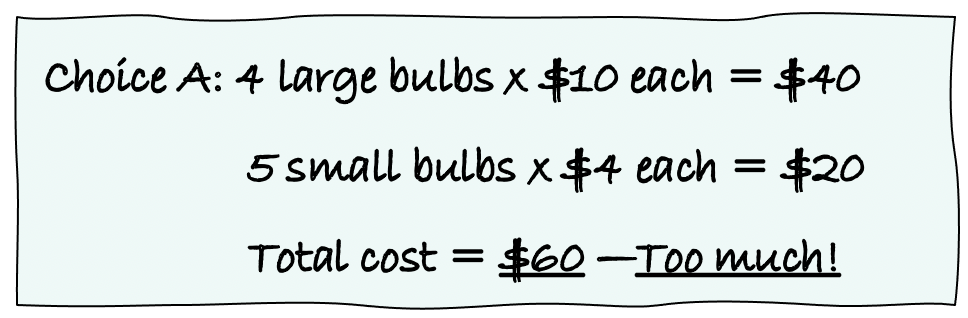
(Remember, the question said Mark wants to spend less than $60, so answer choice a is not correct.)
3. Make a chart. A chart is often an appropriate tool to use strategically. Taking a minute to set up a structure for organizing their reasoning can make the reasoning go faster and make mistakes less likely. There are several quantities to attend to in this problem, so laying out the work in an organized way will make a big difference.
| Answer choice | # of large bulbs | Cost of large bulbs | # of small bulbs | Cost of small bulbs | Total cost |
|---|---|---|---|---|---|
| A | 4 | $40 | 5 | $20 | $60 |
| B | |||||
| C | |||||
| D | |||||
| E |
I’ve started the chart for you, but you can finish it. Pay attention to where you see regularity in repeated reasoning. How is filling out this chart similar to plugging in values for x and y in the inequality given in the problem? How is it different?
By the way, students and teachers can have a lot more fun and learn a lot more from a scenario like this by exploring it in more open ways than are seen on a multiple-choice test. Asking what combinations of bulbs Mark can buy is much more interesting than asking whether or not he can buy specific combinations. How could you and your students explore that question? What concepts and understandings might come to light through that exploration? What other questions might you ask? (I’d start by asking why he can spend under $60 but can’t spend exactly $60!)

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
