Blog

Will This Be on the Test? (Oct 2021)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a high school equivalency test. This month’s installment is a little different. Here’s the question:

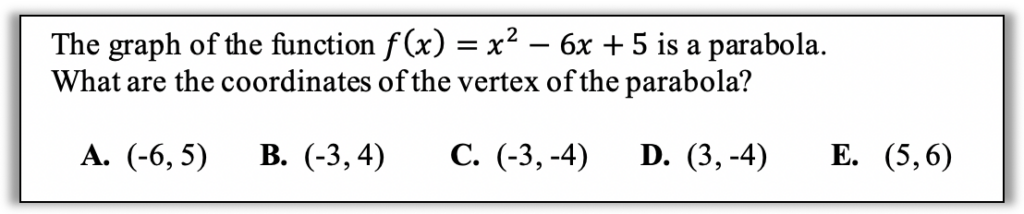
What’s different this month is that I’m not going to ask you to think about different ways you could reason about this question. I’m not going to lay out for you a variety of visual and conceptual approaches based on understandings that are accessible to students working at multiple levels. Instead, I invite you to think about how this question makes you feel – and how it might make your students feel.

If something like this makes your eyes cross or your head spin, you are not alone. If this makes you feel anxious because you don’t know how to do it or fear your students won’t be able to do it, you are not alone. If you feel like you should be able to do this but just can’t remember what you are supposed to do, you are not alone. For many teachers, and for even more students, there are words and notation in this problem that are unfamiliar or long-forgotten. Function? Parabola? Vertex? And what am I supposed to do with the letter f ?!

There is likely enough unfamiliar vocabulary and notation here that making sense of the problem is not possible given the limited time a student has on the test. Sometimes that happens – and it will happen to your students when they go in to take the test. They will encounter questions on concepts that you did not teach them. They will encounter questions that they cannot make sense of because of unfamiliar vocabulary or notation or because they simply have not learned the concept the question is testing.

There is a simple solution to this issue – make a quick guess and move on. The key for a student is being able to discern which questions are worth their time and which are not. The presence of a variable doesn’t necessarily mean a question is out of reach, but when the question might as well be written in a foreign language, it is not worth a student wasting their precious time trying to wrangle with it. Nobody can answer with certainty a question they do not understand.

Students should learn to read a question and ask themselves if they can make sense of the math in the question. Sometimes unfamiliar vocabulary does not have to be a barrier. For example, if I tell you a gobnabbler machine can produce 16 herbledingles every 5 minutes and ask you how many herbledingles two gobnabbler machines can produce in 3 hours, you can probably reason through that without ever knowing what a herbledingle or a gobnabbler machine is. On the other hand, if a question requires you to evaluate an expression like log₃(81) and you have never seen anything like that before, there isn’t a lot to be gained from trying to figure out or guess what it means in a high stakes, timed situation. It is up to the student, in the moment they are faced with a question, to decide if it is worth their time, but they should go into the test knowing that not every question will be and that that’s okay. You might even work that into any test practice you do – the first step in tackling a problem is deciding whether to tackle the problem at all.

It is important that we and our students recognize that it is not feasible most of the time to prepare students to get a perfect score on their math HSE test. A perfect score should indicate that they have the equivalent of a full high school education, something that takes four years in the life of a teenager whose primary job is to attend school. For adult learners who enter our programs often needing to learn topics found at the middle-school level or below, they just don’t have the time or resources to learn everything that is on the test. We must accept that we will not teach everything that is on the test, and we need to help our students accept that as well.

There are two questions I believe are important to ask when deciding whether a student is ready to take the test:

• Are they prepared to pass the test by using problem solving, reasoning, estimation skills, and good test-taking techniques?

• Are they prepared for their next life step (college, career path, new job, etc.)?

These are the things that matter. They matter a lot more than making sure students are prepared to answer every possible question they might see on the test. If the answer to the second question is no, then passing the test and exiting their program does not equate to success beyond school. For the good of our students, we need to take a broader view than only focusing on test scores. A conceptual approach to teaching math, numeracy, and problem solving prepares students for the test and for life, but we all have to be willing to let go of some questions and topics so students can bring their reasoning power to bear on those questions they can make sense of.

There’s another important point here for teachers. In continuing to grow your own mathematical minds and teaching skills, you will do better by your students if you focus your learning on conceptual understanding and problem solving at the level your students are working than if you struggle through higher-level and more abstract concepts until you are sure you could get a perfect score on the test. For many people teaching math to adult learners, those high school-level math skills are decades in the past, and maybe they didn’t make sense even then. If you can’t answer the question at the top of this post, that has no bearing on your qualification to teach math to adult learners. It is more important to be able to model critical thinking, curiosity, and a growth mindset for your students than to be able to demonstrate how to reckon with parabolas. It is more important to grow your own conceptual understanding and flexible thinking abilities so you can nurture those qualities in your students than it is to be able to explain how to solve every question on the test.

If this month’s post didn’t scratch that conceptual itch and you need a task to sink your teeth into, here’s a preview of next month’s question:

What skills and concepts do you think students need to be able to reason about this question? What conceptual and visual strategies can you think of? Tune in next month for the discussion of this question!

---

---