Will This Be on the Test? (Sept 2021)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a high school equivalency test. This month let’s dig into some probability – a topic that many students don’t get to because it often is near the back of the book. But a basic understanding probability is important for general numeracy and it doesn’t take a lot of study of the topic to understand enough to make some sense of probability in the world and to pick up a point or two on the test. In fact, connecting probability to beginning fraction ideas, including benchmarks, can help strengthen both concepts. Take a look at this month’s question:
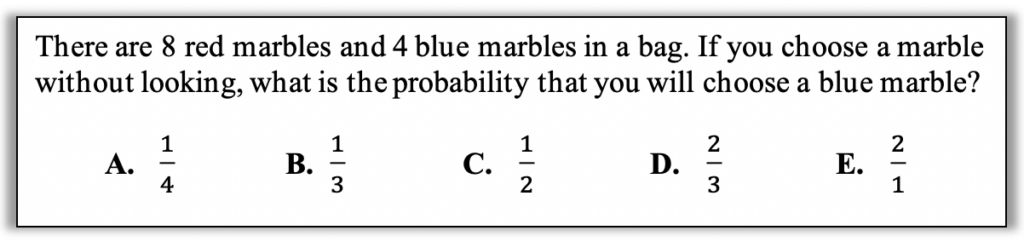

Before you read further, allow yourself to bring your full mathematical reasoning power to bear on this challenge. How many strategies can you think of? What visuals could you use to help you solve this? Also ask yourself, what skills and understandings do students really need to be able to answer this?
You may have learned that there is a formula for calculating simple probability, but let’s see what strategies a student might use if they had some beginning ideas about the concept but hadn’t actually learned that formula.
1. Estimate. Have you noticed a pattern in these blogs? Being deliberate about estimating is a way to develop the habit of making sense of a problem before grabbing a calculator or a formula. In this case it’s invaluable because there are several very tempting wrong answers waiting for a student who is in a hurry. A student who pauses to make sense of the problem and estimate will quickly realize that since there are fewer blue marbles than red ones in the bag, picking a blue marble is less likely than picking a red marble. This means the probability of picking a blue marble must be less than half, narrowing their options to only two.
What understandings does this require? Students should have an idea of the meanings of these probabilities:

Impossible – probability is zero (0%)
Unlikely – probability is a small fraction or percent (more than zero but less than half)
As likely as not – probability is ½ (50%)
Likely – probability is a large fraction or percent (more than half but less than one)
Certain – probability is one (100%)
See the connection to benchmark fractions? Connecting benchmark probabilities to benchmark fractions early on will set up students to make a good estimate on a problem like this and to get a handle on probabilities they encounter in the real world which can help them make informed decisions on anything from whether to bring an umbrella on a walk to whether to get a vaccine!
2. Play “what if?” A student who has gotten off to a good start with an estimate might evaluate the two reasonable answer choices by asking, “what if?” What if the probability of picking a blue marble were 1/4? What would that mean? It would mean that I would expect to pick a blue marble about 1/4 of the time if I played many times. Does that make sense with what I know about the marbles in the bag? Looking at what’s there, would I expect to draw a blue marble about one time out of every four or about one time out of every three?
This line of thinking requires another basic understanding of probability: probability tells you what to expect if you do something many times. Things that are unlikely can happen but usually don’t. Things that are likely might not happen but usually do. To build this understanding for your students while strengthening their knowledge of benchmark fractions and percents at the same time, check out Will It Rain Tomorrow?, a complete contextualized lesson created by the SABES Math Center.
3. Draw a picture – make groups. Even though the problem states that you are supposed to pull a marble from the bag without looking, a student who wants to get a visual handle on the situation can do so by drawing a simple picture using letters to stand for the marbles and make groups like this:

In this picture, each group has only one color of marbles in it and all the groups are the same size. How does this help with understanding the probability? There are three equal groups and only one of them is blue. In other words, one out of three groups is blue meaning you might expect to draw a marble from the blue group about 1/3 of the time.
4. Draw a different picture – make different groups. Here’s another useful way of visualizing the marbles. To make this drawing, a student might start by drawing the four blue marbles each at the top of a column and then filling in the eight red marbles underneath, keeping the columns even as they go.

In this picture, there are four groups that all look the same. Each has one blue marble and two red marbles. In other words, one marble out of every three in the bag is blue. While the fraction or probability 1/3 was hard to read in the problem, it is a lot more apparent in the pictures.
When first looking at this problem, a student might be drawn to answer choices like 1/4, because there are half as many blue marbles as red, or 1/4 because there are four blue marbles in the bag. In fact, the correct answer choice might be the one a student would be least likely to guess because the fraction 1/3 doesn’t seem to be anywhere in the problem. But with a little reflection and visualization, those initially tempting answer choices don’t make sense. It’s worth taking the time to build in probability concepts as you teach fractions and percents to prepare students for the test and to build numeracy and confidence with real world math.

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
