Blog

Will This Be on the Test? (October 2024)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test.

This month’s question involves decimals. I’ve heard students say that decimals are much easier than fractions because they can manipulate them with calculators without having to learn any complicated sequences of buttons. However, just because decimal computations are more accessible on a calculator, that doesn’t mean that reasoning about decimals is “easy.” When calculators are available on a test, students should use them strategically to make computations quickly and accurately, but they should not pick up the calculator until they have made sense of the problem and have good reasons for doing the computations.

Just for fun, let’s imagine that this question is on a section of a test where calculators are not allowed. Can you figure it out without a calculator?

Here’s this month’s question:

Here are some possible approaches:

1. Make sense with a visual. Making sense of the story is a key first step. Drawing a bar model of the given information is one good way to get started because it helps make visible the relationships between the numbers in the story and what is known and unknown. 

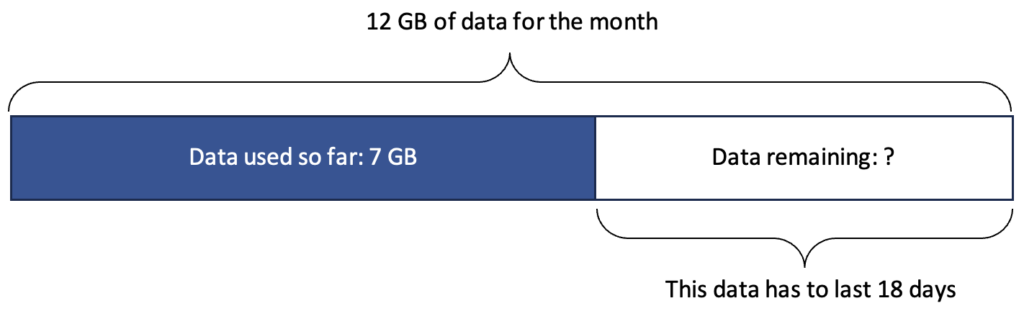
This picture is a way of showing what was described in words. Does it help you make sense of the quantities and relationships in the story? Does it give you ideas about strategies to pursue? Would you illustrate it differently?

2. Estimate! Having established that 5 GB of data has to last 18 days (through making sense!), what can you conclude, without doing a lot of calculation, about the amount of data Nora can use per day? One way to estimate is to do a sort of informal guess-and-check with friendly numbers (benchmarks) to narrow down your idea of what’s reasonable:

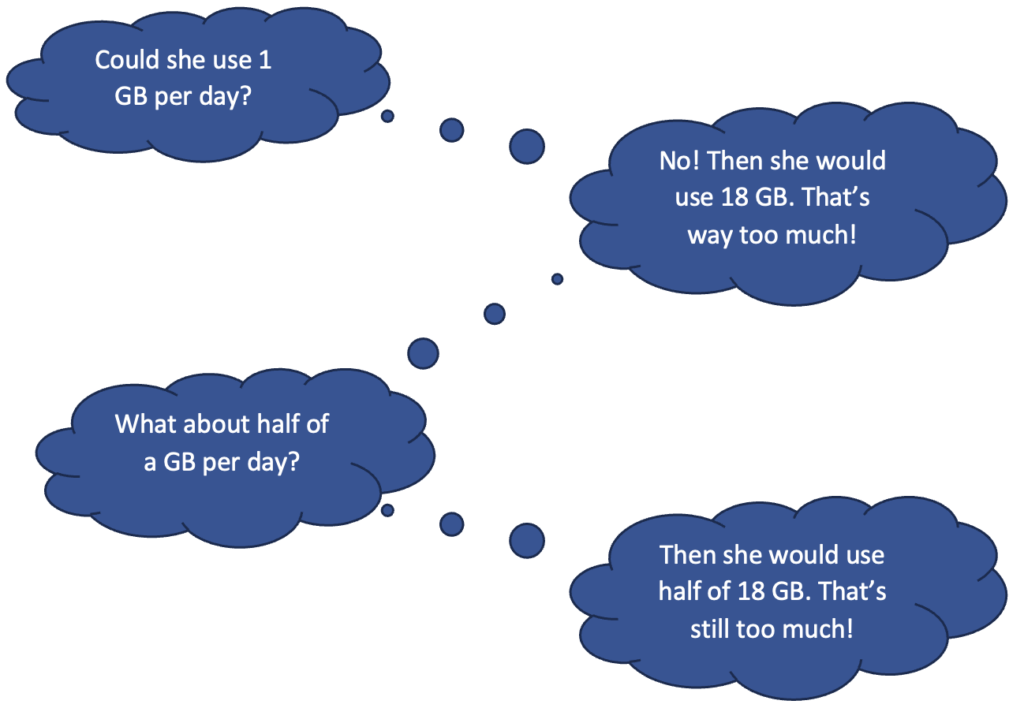
3. Play “What if?”. The question is how many GB of data Nora can use each day without running out, and the answer (to the nearest tenth) is one of five numbers given. What could you do with each of those numbers (or with the ones that seem reasonable) to find out if they are the answer to the question? You might ask:

If Nora uses _____ GB of data every day for the rest of the month, how much data will she use?

How is this question similar to or different from the question as it was asked originally? If this question feels more accessible to you, then this could be a good strategy for you. What understandings are needed to be able to reframe the question?

4. Divide a little bit at a time. One way to make sense of this story is that Nora has to divide up her remaining data among the 18 days that are left in the month. If you don’t have a calculator or just want to think about the division conceptually, you might imagine evenly distributing the 5 GB available among the 18 days by putting data into each day a little bit at a time:

Day	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
GB	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1

So far that’s only 1.8 GB… I can add a little more to each day.

GB

0.1

0.1

0.1

0.1

0.1

0.1

0.1

0.1

0.1

0.1

0.1

0.1

0.1

0.1

0.1

0.1

0.1

0.1

Now I’ve put 0.2 GB in each day, and I’ve used up 3.6 GB all together. How much should I add to each day next?

GB

Try putting another little bit of data in each day. Do you think you can fit another 0.1 GB in each day without going over 5 GB? Why or why not? Does this feel like division to you? What other operations do you see in this approach?

At first read, this may seem like a two-step problem involving first subtraction and then division, and it certainly can be done that way on a calculator. However, not all approaches require thinking about this as a division story! A class discussion that involves both multiplication and division strategies will help introduce or solidify the relationship between multiplication and division, which will increase fluency with both.

---