Blog

Will This Be on the Test? (October 2022)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test. Here is this month’s problem:

Before we get into some possible conceptual and visual approaches to this task, take a look at how a student approached it and explained their reasoning:

What do you notice about the student’s reasoning? What do you wonder?

Did you see that the student used a “key word” to tell them what operation to do to solve the problem? Do you agree that subtraction was the “right” operation to use? Do you agree with the student’s answer?

Let’s take a look at some other ways the student could have approached this.

1. Make sense of the problem/Think about what is reasonable. Taking a minute to think about what you know, maybe even to retell yourself the story in your own words, may bring the relationships between the numbers in the problem to light in a way that scanning for and applying key words will not. The problem states that there is a 35-year age difference between Paulina and her son. Before choosing an operation to apply, a student might follow a train of thought like the one below to restate the information in a more accessible way. For example, they might reason like this:

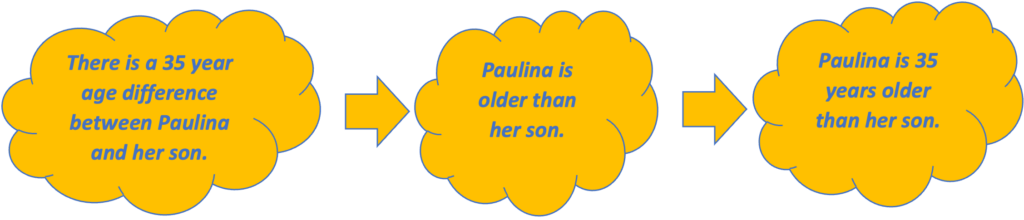
How might this framing affect what math the student chooses to do?

2. Use a number line. A number line diagram may make it clear which of the answer choices are reasonable and which mathematical operation or operations will get a student to the right answer:

3. Use a bar model (also called tape diagrams or Singapore strips). Using one bar to illustrate Paulina’s age and one to illustrate her son’s age will also give a student an idea of what computation will help them find the missing information:

4. Make an analogy to a situation where all the information is known. If I were trying to figure out this problem and I didn’t know where to start, I might think of a similar situation in my own life and use that to figure out the relationships between the numbers in the problem. For example, I am 46 years old, and my nephew is 7 years old. I have to do a little bit of work to figure out the difference in our ages, but it doesn’t take me long to figure out that I am 39 years older than him. Put another way, our age difference is 39 years. Now I can ask myself, if I knew my nephew’s age and our age difference, how would I figure out my own age? If I’m not sure, I can even play around with trying different computations and see which gets me to the right answer. (Because in reality, I already know how old I am!) Once I understand what works in my own situation, I can apply the same reasoning to the problem.

Now that we’ve been through some possible sense-making approaches, look back at the student work at the top of this post. How might other approaches have helped them make sense of the problem? Did the “key word” approach help or hinder?

All of the approaches above require a degree of student agency. Students often ask in math class, “Am I allowed to… ?” Or, upon seeing diverse approaches, students might react by saying something like, “You didn’t tell me I was allowed to draw a picture!” Students must be empowered to do more than just read and respond to a problem. Students who can reframe, illustrate, or make analogy to the context of the problem can open up many possibilities for solving it. They need to know that they do not need to ask permission to engage with the problem in their own way.

Here’s a bonus for this month. Take a look at another student’s approach to the same problem. How could you support this student’s reasoning and help them build on it?

---