Will This Be on the Test? (November 2023)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test. Here is this month’s question:
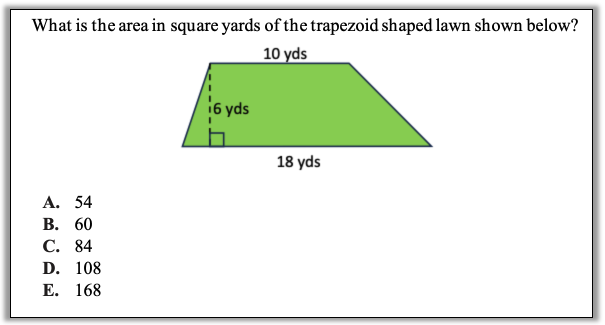

How can you approach this question in a way that makes sense to you? What conceptual understandings or visual tools can you bring to bear? What mathematical concepts do students really need to be able to tackle this problem? How might your real-world experience help you reason about this?
You may be thinking that the one and only way to answer this question is by using the formula for the area of a trapezoid, which is on the reference sheet for both the HiSET and the GED. There was a time when I would have thought that as well. But if you have been reading this blog series, you know that there is never only one way to approach a math task. Here are some approaches that do not require using the formula page:
1. Estimate from the inside and the outside. A student who has not had experience with trapezoids may still be able to reason about the area using ideas about rectangles. For example, a student could reason that the area is bigger than a rectangle that fits entirely inside the trapezoid:
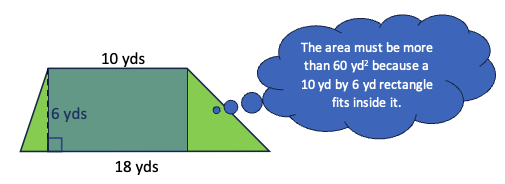
And smaller than a rectangle that the trapezoid fits inside:
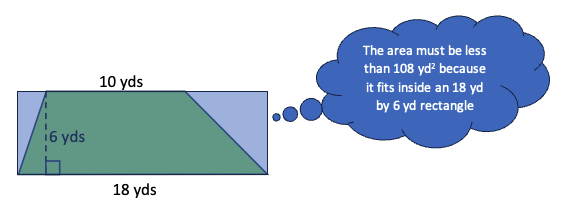
2. Estimate by finding a shape with a similar area. A student could also eyeball a rectangle in between the two in the first strategy and use that to estimate the area like this:
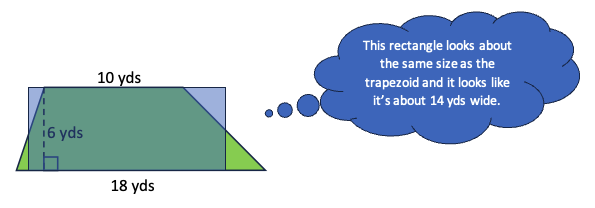
3. Chunk it up. A student who has explored the areas of triangles might try to be more precise by breaking the trapezoid into a rectangle and two triangles and finding the areas of the three pieces. Note that they would have to guess at the bases of the triangles. I encourage you to experiment with different guesses and see how that affects the answer you come up with.
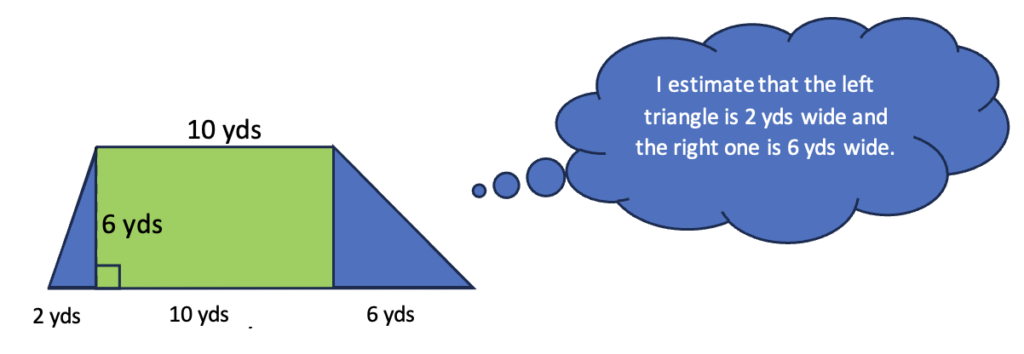
(What geometric understandings go into making this estimate?)
4. Chunk it up from the outside. A student could start with a rectangle that encloses the trapezoid and estimate the widths of the extra triangles to find the areas to subtract:
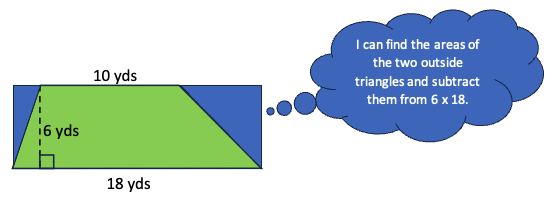
How do the outside triangles in this strategy compare to the inside triangles in the last one?
Looking at these four strategies, or thinking of another that isn’t here, you might think one is easier than the others and that is the one you should teach to your students. However, the easiest strategy is the one that makes the most sense, and that will be different from person to person. And consider the geometric insights that could arise from a conversation that explored all of these directions.
You may be wondering why I would encourage you to look beyond the formula page. having the page can feel like a gift, but I think it can lead us astray in our priorities (at least it did for me in my early teaching days). I taught my students to read it like a recipe: the elements of the formula were the ingredients they had to gather and then the formula would tell them how to put them together. While this approach does work, looking back I have two issues with it. One is that it doesn’t make room for thinking about what kind of answer might be reasonable or for estimating. It’s simply a matter of “plug and chug”, not making sense. The second is that it isn’t as easy as it seems because it’s not always clear what the meanings of the “ingredients” are or how to apply the formula. For example, the HiSET page gives this as the formula for the area of a trapezoid: Area = ½(base1 + base2)(height). In order to use this formula, students have to be able to make sense of the terms and notation in it. They have to know what parts of the shape the words and symbols in the formula refer to. It is a strain on memory instead of an application of reasoning (not to mention that sometimes it is not trivial to figure out which formula to use in the first place).
Learning to be fluent with applying formulas reliably is as much work as learning to approach questions flexibly and creatively, but the latter has a much bigger payoff beyond test day.

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
