Blog

Will This Be on the Test? (Nov 2021)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a high school equivalency test. Last month we looked at a question that looked so abstract and complicated that most students would be better off skipping it than trying to figure it out. This month’s question might seem to fit in the same category, but it may be more accessible than it first appears:

For the purpose of this exploration, I’m going to skip over strategies that involve following the steps of solving algebraic equations. Instead, let’s see how far we can get with two important understandings that can be built over time in almost any level class. (See Meeting the Needs of Numeracy-Level Math Students for more about the needs of students at the most foundational levels.)

Understanding #1: An equation is “true” when the value on each side of the equals sign is the same. This is not a trivial understanding. Many students have the mistaken idea that an equals sign means “do the calculation and put the answer on the other side.”

Understanding #2: The letter in the problem above (x) stands for a number; there is a number that x can be replaced with that will make the equation true. Students can begin to build comfort with using letters to stand for numbers early by capturing their own generalizations in more formal notation. For example, a student who understands the perimeter of a rectangle as being twice the length plus twice the width can learn to express that relationship as an equation with variables: 𝜬 = 𝟐 × 𝑙 + 𝟐 × 𝑤.

These two understandings take time to build but can be integrated into almost any mathematical exploration. Do not be afraid to introduce variables and equations to your students in small doses with strong connections to concrete understandings. This will provide a much smoother path for them than one day beginning an algebra unit and introducing the concept of using letters to stand for numbers all at once.

Armed with these fundamental understandings, here are some ways a student might approach this question.

1. Visualize equivalent fractions with bar models. This question looks like a statement about two equivalent fractions, even though one of them has some weirdness going on in the numerator. Setting aside that concern for a moment, a student might try to make sense of the equation by drawing a picture of the fraction 2/3 and comparing it to a model showing 15ths:

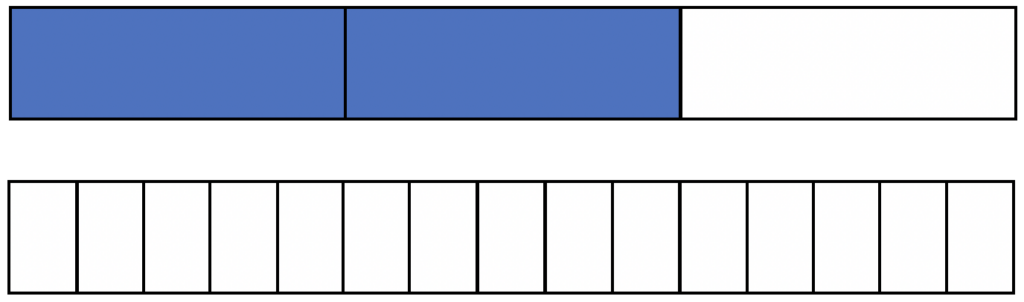
Since the equals sign means that the values on either side must be the same, the number of 15ths must be such that the two fractions are equivalent. The number of 15ths is 𝑥 and 3 more (𝑥 + 3), so a student might count off three blocks on the bottom and then see that the remaining number of blocks is the value of 𝑥.

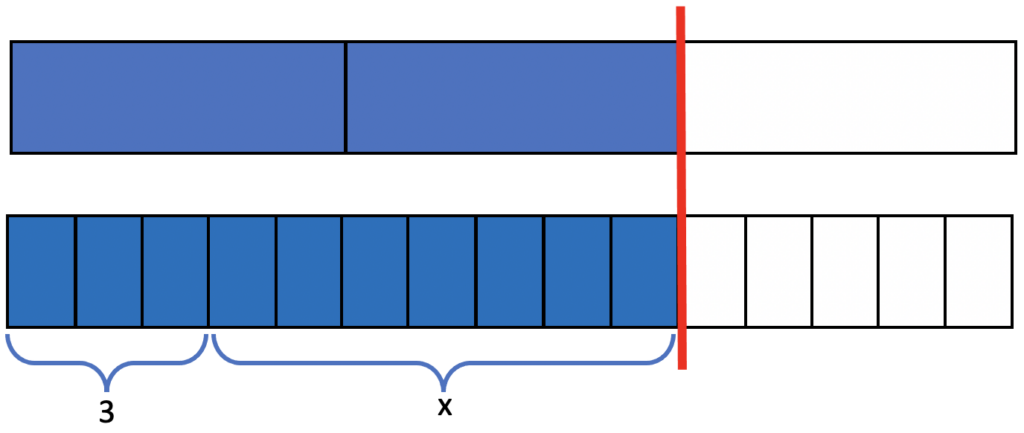
2. Reason about equivalent fractions by multiplying the numerator and denominator by the same number. Students who have developed conceptual understanding of equivalent fractions through working with concrete and visual models (like the bar models above) may reason more abstractly like this:

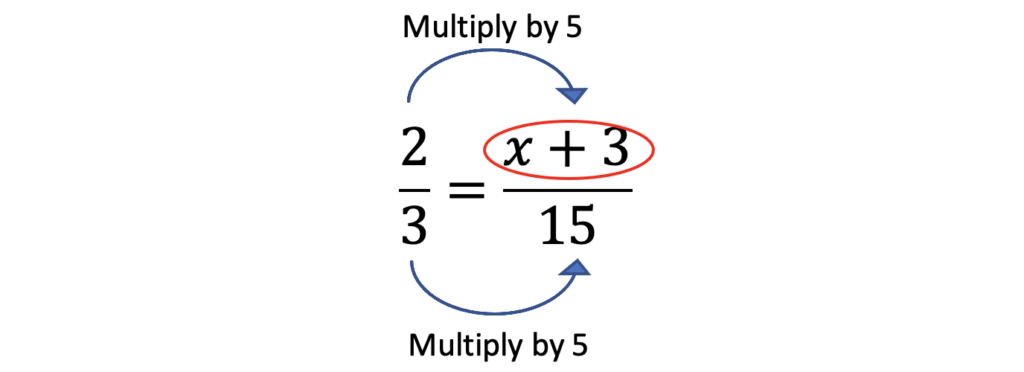
This means that the value of the circled expression must be 10. At this point a student might ask themself, what number can I add to 3 to get 10? That must be the value of 𝑥 that makes the equation true.

3. Reason about equivalent ratios by making copies of ratios. A student might see this equation as a statement about equivalent ratios instead of equivalent fractions, opening up another avenue of reasoning. The student might make copies of a ratio of 2 to 3 until they had a ratio of something to 15:

As in the first approach, the number of circles is 𝑥 and 3 more, so the circles can be put into two groups – one with 3 circles and the other with 𝑥 circles

There is one more step in solving an equation by any strategy – checking the answer. While algebra can be intimidating in many ways, one thing it has going for it is that you can always tell if you have found a correct solution by substituting the value you found for 𝑥 in the original equation. Students who understand the notation in an equation can even navigate a multiple-choice algebra question like this one by just trying out each answer choice – but reasoning is better because life is not a multiple-choice test!

---

---