Blog

Will This Be on the Test? (May 2023)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test. Here is this month’s problem:

As with many test questions, it is not immediately clear in which textbook chapter this question might fit. Questions about ladders often show up in lessons on the Pythagorean theorem, but just as often they show up in lessons on similar triangles. This question has something to do with angles, so maybe it belongs in an angle lesson. In a test situation, though, a more useful direction for a student to pursue is to make sense of the question in general rather than to try to figure out what kind of math they are “supposed to” use to solve it. One of the big challenges of standardized tests is that the questions come from all kinds of areas of math and don’t necessarily target the skills students have just been working on.

So, here are some possible approaches:

1. Investigate structure. A student who doesn’t know what they are “supposed to do” with a question like this might start by asking themself how ladders leaning against walls work in general. What affects the angle the ladder leans at? If the angle is going to stay the same, what else changes when the length of the ladder changes? A sketch helps:

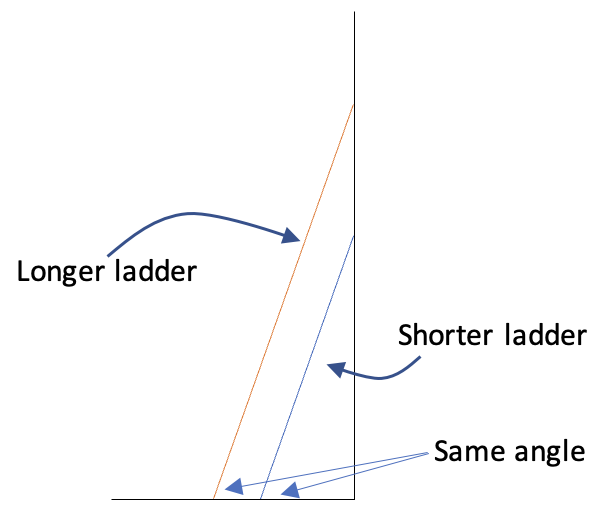
What do you notice in this sketch? How might this help a student make an estimate or choose a strategy?

2. Estimate with a sketch. You might recognize similar triangles in the sketch above, or you might not. Even if the sketch doesn’t give a student a clue about what textbook chapter this question might fit with, it still could be useful. A student might compare the change in distance from the wall with the change in the length of the ladder:

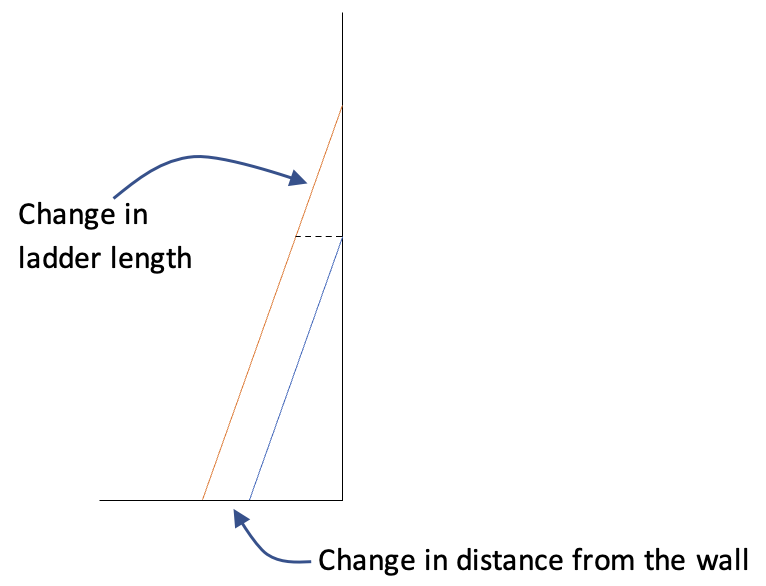
The change in the distance from the wall is smaller than the change in the ladder length. In the scenario in the question, the new ladder is 2 feet longer than the first ladder. What does this mean about the distance from the wall of the new ladder?

3. Reason proportionately with benchmarks and a double number line. A student who knows or guesses that there are some equivalent ratios at play in this question might reason with a double number line and friendly ratios like this:

If an 8-foot ladder has its base 2 feet away from the wall, a ladder that is twice as long would have its base twice as far away from the wall.

I can find the halfway point on each of these number lines to get a new data point.

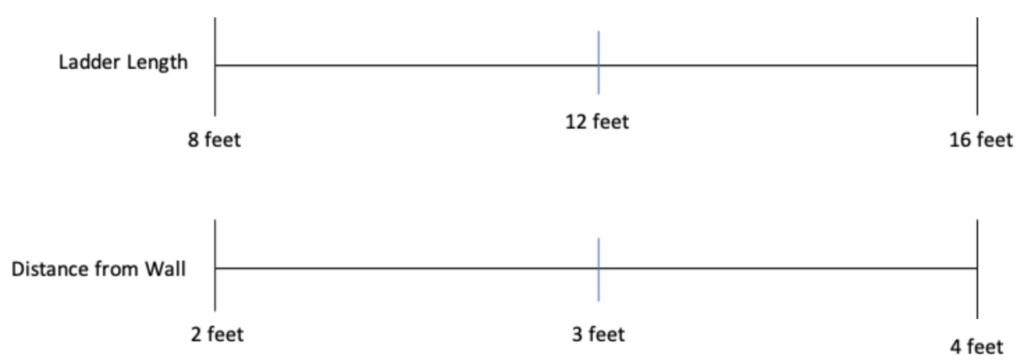
How might the student continue this reasoning to find the distance from the wall of a 10-foot ladder?

4. Reason with fractions or percents. The new ladder is 2 feet longer than the first ladder, but a student who has drawn a sketch and thought about structure will have realized that the distance from the wall will not change by the same number of feet as the ladder. Instead, it might increase by the same fraction. A bar model diagram can help a student see by what fraction the length of the ladder has increased:

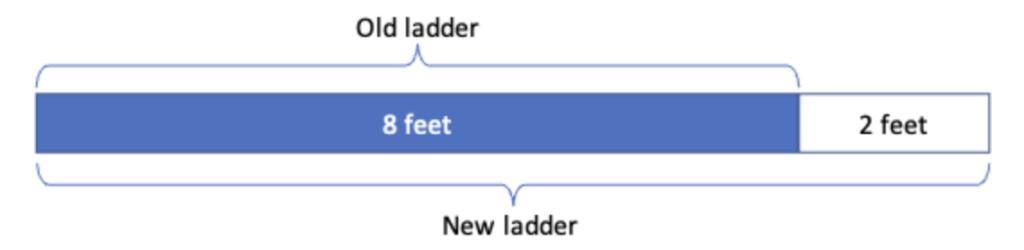
In this case, the difference between the old ladder and the new ladder fits neatly into the old ladder exactly four times, like this:

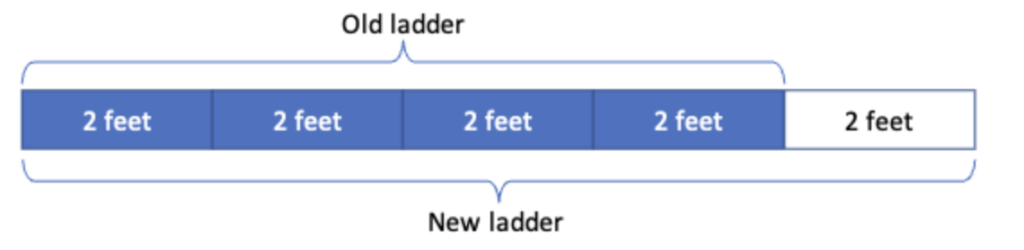
There are many ways a student might describe the relationship shown in this model. For example:

• If you divide the old ladder into four equal pieces, the new ladder is five times the length of one of those pieces.
• You can get the length of the new ladder by adding on one-quarter of the length of the old ladder.
• The new ladder is 25% longer than the old ladder.
• The new ladder is 1 ¼ times as long as the old ladder.

They then might apply the same relationship to the distance between the wall and the base of the ladder. This could be done abstractly, working only with numbers, or they might draw a similar diagram to apply this relationship to the distance between the wall and the base of the ladder:

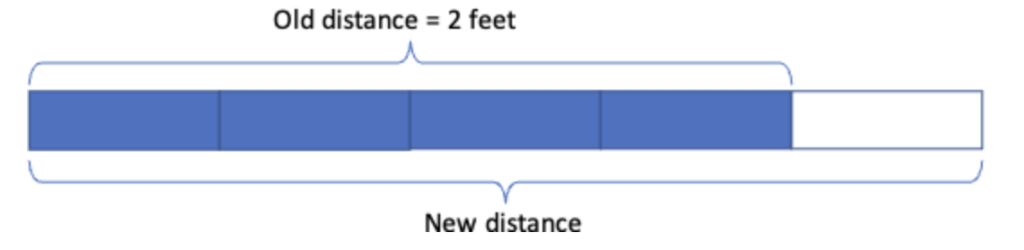
How can you fill in the boxes in the diagram using the given information?

Standard for Mathematical Practice number one is “Make sense of problems and persevere in solving them.” The first step in making sense of a problem can be to identify what kind of math the question involves, but it doesn’t have to be. Drawing pictures is a great way to start making sense of a problem, especially if the question involves a real world situation that can be sketched relatively easily. Pictures can open doors to many more approaches than what might be found in a textbook.

---