Will This Be on the Test? (May 2022)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test. Usually when we explore a test-like question in this column, there are multiple possible approaches and strategies students can use to arrive at an answer or a very good guess. Students may draw pictures or make charts, use guess-and-check strategically, estimate, and more. However, not every test question calls for deep reasoning. Take a look at this month’s question below.
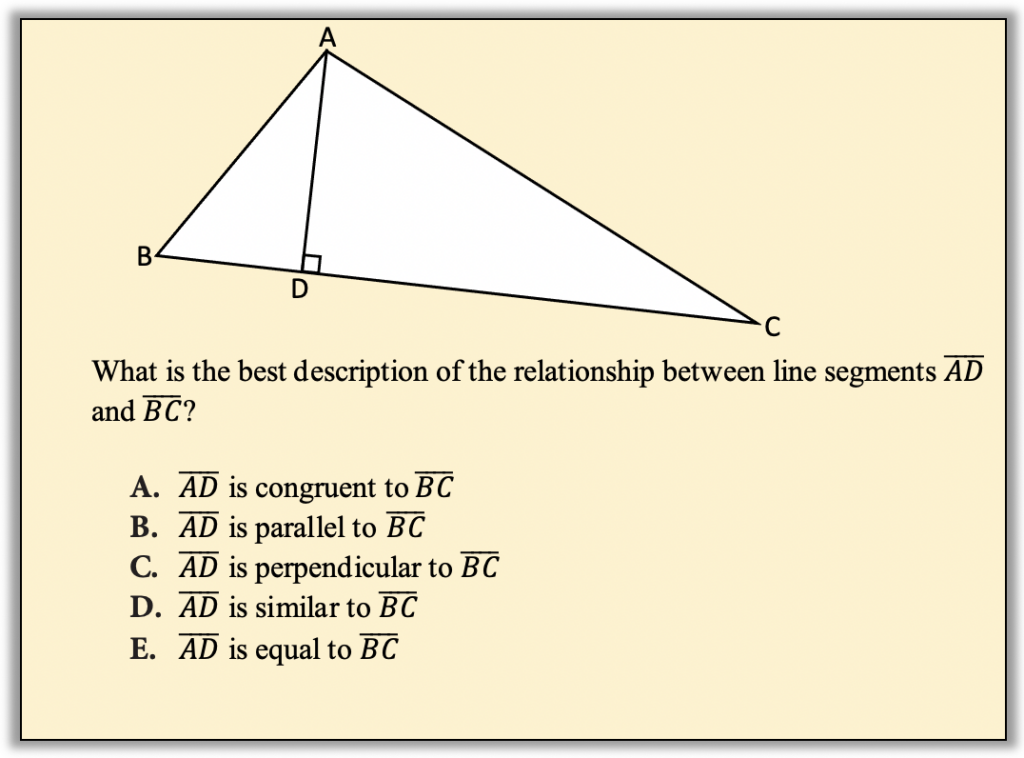

Pause to reflect. This is where I would usually ask you what skills and understandings are needed for this problem and how many approaches you can think of that might be accessible to students at a range of levels. However, with this question, the focus is on vocabulary and there isn’t all that much to figure out. The student needs to recognize the relationship between the two line segments and they need to know the name for it. So, instead of pondering how to approach this problem conceptually, I ask you to ponder how it might be possible to teach vocabulary conceptually.
There is a lot of math vocabulary to learn and it is important that students learn it, both to be able to answer questions like the one above and also to be able to communicate their thinking and understand other people’s thinking. Some people believe it is best to pre-teach or front-load all the vocabulary students will need for a lesson so that they will not be confused or tripped up when encountering unfamiliar words. My opinion is that you will create longer lasting and deeper learning by keeping the focus on the concept and introducing the vocabulary once students have a concept that they need a word for. Understanding a concept before you have the word for it creates an intellectual need for the vocabulary.
Geometry is especially laden with vocabulary and especially rich with beautiful things that that vocabulary can be used to describe. What if, instead of starting off a lesson with a list of long and intimidating words, we gave students some colored pencils and a design like the one below to color on?

What do you see first in the pattern above? How would you describe it? If you want to explore your own ideas before reading further, you can click here to access a version that you can print out and color yourself. After you color, ask yourself how you would describe your findings to someone who couldn’t see your paper. What vocabulary would you need to use?
What do you see? Maybe you see triangles, rectangles, or parallel lines. Maybe you see trapezoids or rhombuses. Maybe you see different kinds of angles. Maybe you see congruence or similarity. With some freedom to color and explore, students will discover many important geometry concepts that happen to have names. Once your class is deep into a rich discussion of the concepts, it becomes a relatively simple thing to drop the important vocabulary into the conversation and students will have a concept ready and waiting to attach it to. For example, suppose I have found the following triangles in the pattern:
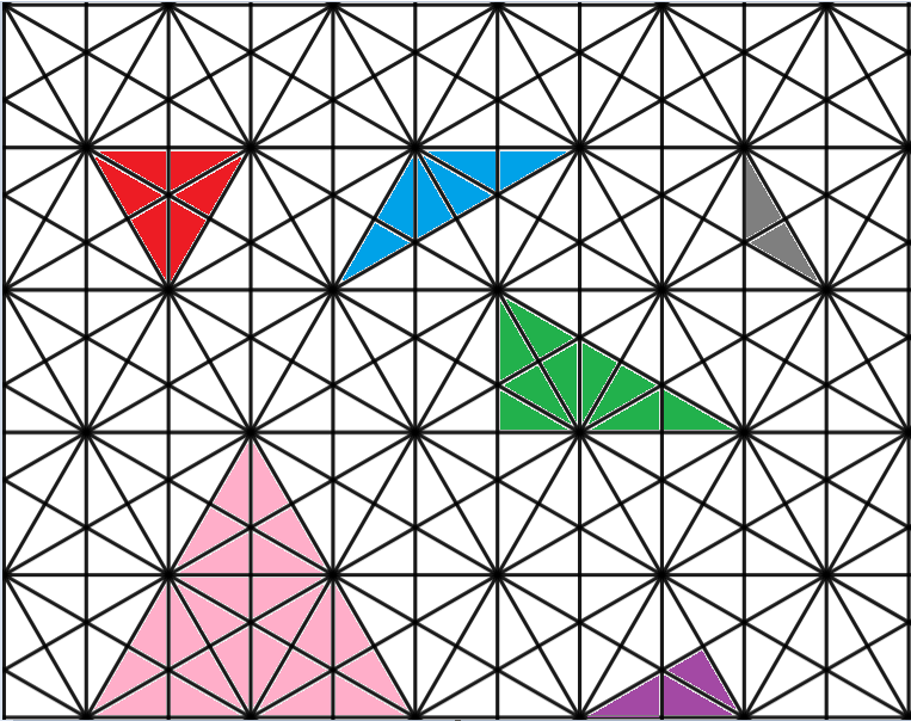
What questions might I ask about my triangles? What vocabulary might I need to talk about them?
Even asking the question, How many different triangles did I find? can motivate important conceptual understandings and vocabulary as I work to make sense of what it might mean for triangles to be “different.” (Do you think I’ve found all the different triangles that are possible to find? How would you argue that I have or that I haven’t?)
What other shapes, concepts, and relationships are present? Starting geometric conversations with What do you see? and moving to How can you describe it? will have students engaged in conceptual learning and ready and wanting new vocabulary to talk about their ideas. Instead of trying to remember that a rhombus is a quadrilateral with four equal sides, and is somehow kind of a square and kind of not, they may remember that “rhombus” is the name for that thing they discovered and why this shape is a rhombus and another one isn’t.
Once some vocabulary is established, a whole new game is possible, leading to questions like How many different trapezoids can you find? How many parallelograms? Where do you see perpendicular lines? How do you know they are perpendicular? and so on.
Vocabulary doesn’t have to be taught separately from concepts and doesn’t have to be dry and intimidating. After deeply exploring the pattern in this blog or other similarly rich geometric objects, would your students be able to identify the relationship between the line segments in our original problem? I bet they would!
Want some online options for explorations that can generate the need for vocabulary? Check these out:
Kaleidoscope – created in Desmos. Students can manipulate the shapes by moving a slider
Polypad – There are a wealth of geometric options to explore at this free resource from Mathigon.org. Note that the button on the right gives the option to use different kinds of grids or arrays of dots as a background.


Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
