Will This Be on the Test? (May 2021)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
In the April 2021 WTBotT blog, I talked about how the data domain encompasses many different kinds of reasoning – number sense, proportional reasoning, and even geometry! This month let’s look at a question from geometry that might come up in a data context. Here is Dericia’s sales graph again, this time with a geometry question:
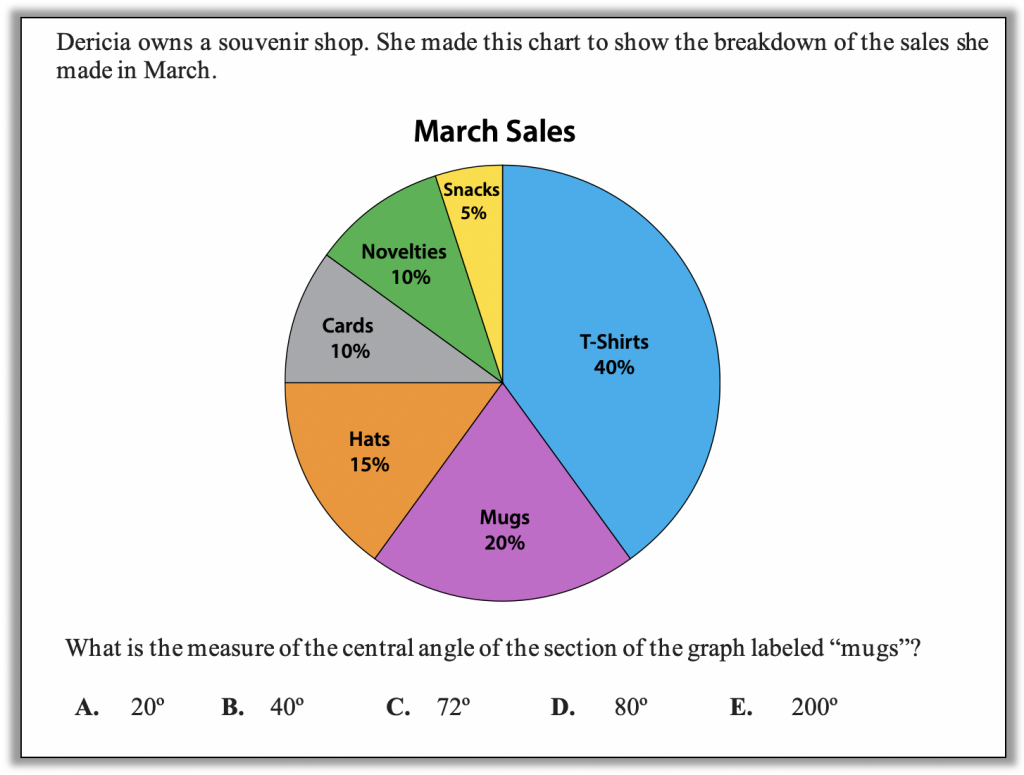

Before you read further, allow yourself to bring your full mathematical reasoning power to bear on this challenge. How many strategies can you think of? What visuals could you use to help you solve this? Also ask yourself, what skills and understandings do students really need to be able to answer this?
Also, here’s something to consider before we get into some problem-solving strategies: why do you think one of the answer choices is 20°? Why might a student pick that answer? It could be partly because of the way the student has been taught. There are a lot of topics to learn in math class, and they are often in isolation and without context. For students with limited conceptual understanding of how math topics and operations relate to each other, it is easy to mix up the rules and symbols. Even a student who can give an answer as a percent when doing a unit on percents and in degrees when doing a unit on angles may mix up the two when they are presented so close together in a high-pressure situation. A student who has not developed confidence in their own ability to make sense of problems and persevere in solving them will likely pounce on the incorrect answer option (a), thinking that if the pie chart piece is 20%, the angle must be 20°.
Now, here are some possible approaches one could use to reason to the correct answer:
1. Estimate! Building familiarity with the sizes of angles, especially by connecting them to things students know in the real world, will prepare students well to eliminate unreasonable answers without the need to do any calculation. A student who can eyeball a 90° angle can quickly assess that the angle for the mugs section is less than 90° but not a lot less. How much less? That’s hard to tell, but since 72° and 80° are the only choices that can reasonably be described as a little less than 90°, the choices are cut down to just two options very quickly – a win in a testing situation!
2. Measure! Even though students can’t use protractors during the test and this question is likely on a computer screen, that doesn’t mean that they can’t still use measuring tools! A quick angle-measuring tool can be made by ripping off one corner of a piece of scrap paper. Using this tool will quickly show how the angle in the problem compares to the 90° of the paper corner. As a bonus, folding the corner in half makes a handy 45° reference, too.

While I’m not suggesting that you teach this to your students as a “trick”, it is reminder that teachers can connect angles to the real world by linking them to things students already know. This can build understanding and prepare them for the test at the same time. Connecting angles to real objects may help students avoid the trap of confusing the percentage in the section with the measure of the angle.
3. Guess-and-check. A nice follow-up to estimating, whether by eye or with a hand-made reference, is to use a guess-and-check strategy to narrow down those two remaining choices to one correct one. A student might reason like this, adding on groups of 20% until they get to 100%:

There are other ways to check these guesses. A shorter way would be to multiply each by five because 20% x 5 = 100%. The important thing is that students can bring their knowledge and understandings to bear in a variety of ways.
4. Reason proportionally! Did you notice that the guess-and-check strategy was another example of proportional reasoning? Proportional reasoning shows up in so many contexts. Teaching it richly and deeply prepares students to use it flexibly in the many contexts in which it arises, both on the test and in their lives. Here are two more proportional reasoning approaches a student could take for this task:
- If 20% is 1/5 of the whole, then the angle must be 1/5 of 360°. Divide 360° by 5 to get the answer.
- Set up and solve a proportion comparing the percent to the whole, and the angle to 360°:
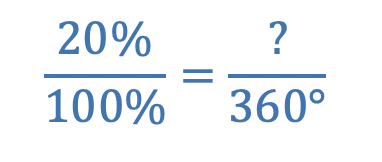
(As always, there are multiple correct ways to set up this proportion and many solution paths beyond applying the cross product.)
Remember, the point of exploring these approaches is not to say that you need to teach your students how to solve this problem using all of methods. Students don’t need to memorize four different ways to solve one problem – they need a solid foundation of conceptual understanding from which they can build a solution path that makes sense to them. Committing to conceptual teaching gives students the tools and confidence they need to find one of these strategies or even to create one none of us have thought of yet!

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
