Blog

Will This Be on the Test? (Mar 2022)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a high school equivalency test. It has been a chilly winter where I am in Massachusetts, so let’s look at a wintry problem this month. (Maybe by the time you’re reading this, you’ll be thinking more about flowers than icicles!)

As you were pondering this question, you may have wondered what domain this comes from. Is this a question about fraction operations? Is it a question about proportional reasoning? As with most substantive problems, this doesn’t boil down to a single application of a single skill. A student facing this problem will need to draw on skills from different math lessons. This is an important thing to consider as we plan our lessons — if we integrate topics, concepts, and skills, students will know how to do the same on a test. If we teach and assess a single skill at a time, we are not preparing students to use their math for problem-solving on a test or in life.

1. Estimate. It’s not easy to make sense of a rate like 2/5 of an inch per minute, but a student who has a strong sense of benchmark fractions may reason that 2/5 is a little less than ½ (because 2 is a little less than half of 5). Knowing that the icicle is growing at a rate of a little less than half of an inch each minute, a student may reason that it grows a little less than 1 inch every 2 minutes.  2½  hours is 150 minutes, so the icicle would grow a little less than 1 inch 75 times (because 150 minutes is 75 groups of 2 minutes).

2. Take small steps. Knowing the rate of growth per minute means that we know how much the icicle grows every minute. A student might make a chart to keep track of the growth of the icicle minute by minute:

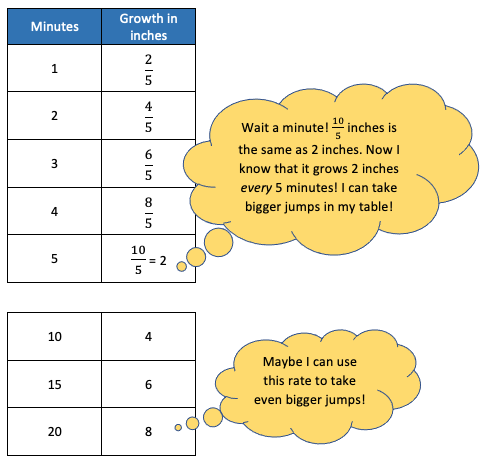
A few notes about this approach:

• It relies on the understanding that non-unit fractions (fractions with a number other than 1 as a numerator, like 2/5 ) are groups of unit fractions (like 1/5) and that you can count by groups of unit fractions. This is a valuable and demystifying understanding of fractions and is important enough to have its own standard. (Understand a fraction a/b with a > 1 as a sum of fractions 1/b. (4.NF.3)) If you aren’t seeing how this table involves counting by groups of unit fractions, take a close look at the pattern in the numerators in the first part of the table.
• It may seem at first like this approach is too time-consuming, but starting with small steps can reveal patterns that make bigger steps possible and shorten the work.

3. Chunk up the time. A student who arrives at the conclusion that the icicle grows 2 inches in 5 minutes may also start to think about how many groups of 5 minutes are in 2½ hours:

4. Multiply the number of minutes by the amount the icicle grows in each minute. Of course we can use a procedure to multiply 2/5 of an inch per minute by 150 minutes, but let’s look at what it can look like with a picture instead. We’ll use bar models to make 150 groups of 2/5 (or at least to get an idea of what it might look like if we made 150 groups.)

• Here is one group of 2/5, representing one minute’s growth in inches:

• To see two groups of 2/5, we can color in two more blocks. This is 2 minutes growth — still less than one whole inch.

• For a third group, we will need to add in another bar. In three minutes, the icicle will grow 1 1/5 inches.

• It looks like we can fit two more groups into the model above. Here is a picture of 5 groups of 2/5. This is 5 minutes worth of growth — a total of 2 whole inches.

How would you continue this multiplication model? What connections can you make between this visual and the chunking strategies above? What connections can you make to a procedure you know for multiplying fractions?

Several of these approaches involve reasoning proportionally in increments to get to a final answer. One thing I love about this kind of approach is that it gives the reasoner flexibility to choose the size of the steps they want to take. Look back at strategies 2 and 3. Would you make the same decisions about when to jump to bigger chunks or what size chunks to use? Why or why not? What seems easiest or most efficient to you may seem harder or less efficient to someone else. When I reason this way, I don’t always take the same size steps — it depends on the numbers I’m dealing with and on my whims! Empowering students to be flexible in their proportional reasoning makes them stronger reasoners and positions them as thinkers instead of mere followers of someone else’s rules.

---