Blog

Will This Be on the Test? (June 2024)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test.

This month we’re back in the realm of fractions—the topic that seems to trouble possibly more teachers and students than any other. There are so many procedures connected to fractions and they can be counter-intuitive. If students can’t see any good reason why they have to find a common denominator in some situations but not in others, or why they sometimes (but not all the time) have to flip one fraction over, they might give up on trying to remember all the rules and instead resort to guessing or applying whatever steps come to mind first. Unfortunately, the gimmicks, tricks, cartoons, and songs we learn to remember fraction procedures don’t hold up in the long term.

The good news is that fractions can make sense! When students start with concrete and visual understandings of the meaning of fractions, they can build solid and lasting understandings of how they work.

Consider this month’s question:

Even a student who knows their fraction operation procedures cold may not know what to do here. There are two fractions and one whole number, but what operation is called for? Here are some strategies that start with making sense of the problem instead of jumping to an operation:

1. Make sense and estimate with benchmarks. A student might start by making sense of the first part of the question using benchmark 1/2. 

And they might continue their reasoning by considering benchmark 1/4.

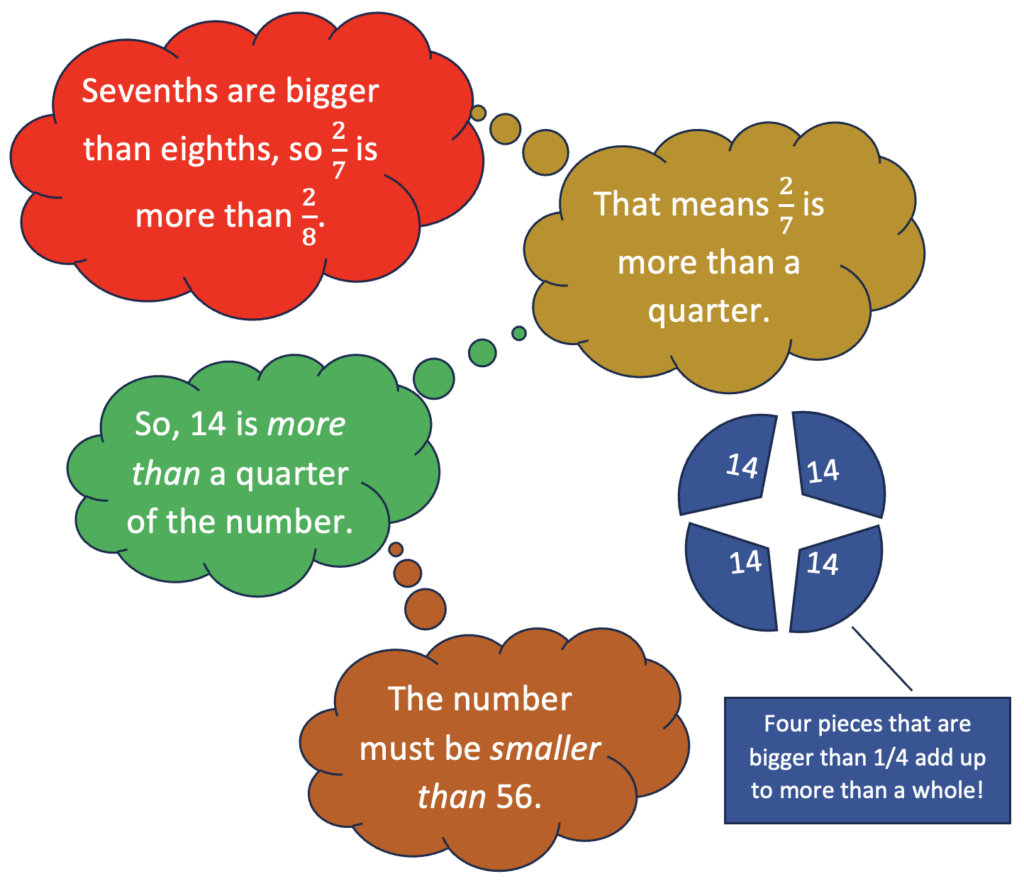
And finally, the student might think about finding 5/7 of the whole now that they know the whole is more than 28 and less than 56.

• What benchmarks might be useful in thinking about 5/7? What answer choices seem reasonable now?

• What fraction understandings were used in this making sense approach?

2. Make sense and estimate by thinking about relationships. Another way to make sense of this question is to think about what information you are starting with, and what information you need to find. A student might reason like this:

• What fraction understandings are used in this making sense approach?
• How else might a student reason using the relationship between two pieces and five pieces?

3. Use a bar model or other fraction visual. Another great way to make sense of the information you have and use it to get the information you want is to start by drawing a picture. In this case, here is the information we have:

• From knowing that two blocks in the model are together worth 14, what conclusions can be drawn?

• Can you figure out the value of one block? How could knowing the value of one block help you figure out the whole? Is it possible to figure out what 5/7 of the number is without figuring out the whole first?

• What fraction understandings are used in this sense-making approach?

Problem-solving with fractions often involves reasoning beyond identifying and applying an operation. In the case of this question, none of our strategies required knowing a procedure to add, subtract, multiply, or divide with fractions but they did require fundamental conceptual understanding of the meaning of fractions. This is not to say that it isn’t important to learn how to do operations with fractions, but rather that learning doesn’t have to be trying to memorize a bunch of procedures that feel meaningless. When students begin their fraction journey (or reboot it, since adult learners may already have a painful history with fractions) with building understanding about the meaning of fractions, how to visualize them, how to compare them to benchmarks, and how to think about them flexibly, they will have a strong foundation on which to continue to discovering and constructing ways of reasoning about operations that makes sense to them.

---