Blog

Will This Be on the Test? (June 2023)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test. Here is this month’s problem:

I remember seeing (and assigning to students) pages of problems like this one in an Algebra I class. Students were supposed to define a variable, express all quantities in terms of that variable, write an equation, and solve the equation. That is an approach that works, but since this is a story question and has a context, abstracting it to an equation is far from the only valuable approach. Even though this may be meant to be a question about writing and solving equations, there are other entry points that are available to students who are not yet comfortable at that level of abstraction.

Here are some other possible approaches:

1. Consider reasonableness. It is often helpful to start with benchmark fractions when reasoning about splitting and sharing. A student might ask the question: Did Njeri pay for more or less than half of the gift? On considering that question, which answer choices seem reasonable? Which do not?

2. Start with a fair split and work from there. We don’t know what led Njeri and Andrei to split the cost of the gift unevenly, but for whatever reason Njeri spent more on it than Andrei did, and that means they didn’t split the cost in half. However, starting with splitting the cost in half and investigating from there could be a useful way to figure out how much they each did contribute. A student might reason this way:

3. Guess and check. Because this is a test question, a student might also choose to just check out each answer choice in the story. For example, answer choice a says that Njeri contributed $11. What would this mean about how much Andrei contributed? Since the gift cost $27 all together, Andrei must have made up the remaining amount and paid $16… but this doesn’t make sense because we also know that Njeri paid $5 more than Andrei.

Note that in this guess and check approach we used the total to find out Andrei’s contribution and then checked that against what we knew about Njeri paying more.In the previous approach, we used the fact that Njeri paid more to find out how much Andrei paid and checked that against what we knew about the total amount paid. Because we have two statements about how the two amounts are related, we can use one to find the missing information for a guess and then check it against the other.

4. Use a bar model. Bar models, also called tape diagrams or Singapore strips, are a great tool for analyzing situations where you have information about relationships. In this case, the situation can be modeled by starting with two bars whose value totals $27 with one longer than the other because Njeri contributed more than Andrei:

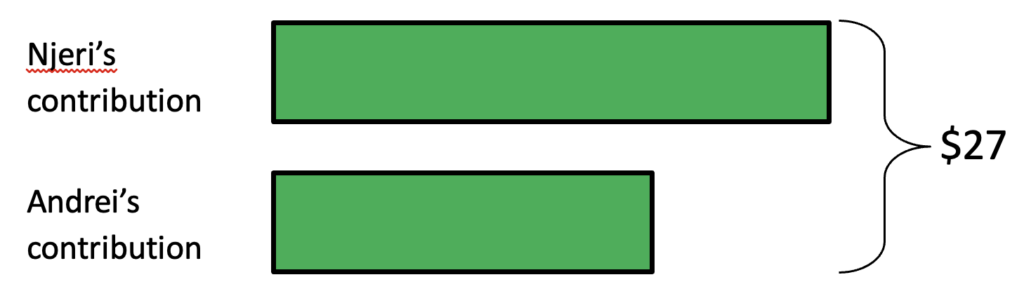
The information that has not yet been added to this bar model is how much more Njeri contributed than Andrei. But we can see where the difference between the two bars is, so all we have to do is label it.

The two unlabeled blocks are the same size. How does the diagram help make it clear what mathematical operations will lead to their value? Once that value is filled in, how will the diagram help answer the question?

Symbolic algebra, in the form of equations, variables, and steps, can be a great tool for answering questions like this, but it is an abstract tool. It is an abstraction of making sense of relationships and reasoning through their implications, as all of the above strategies did. To arrive at a comfortable place with that level of abstraction, students need to start their algebraic reasoning with more concrete and visual approaches. Eventually, abstract symbolic algebraic reasoning will feel like a natural next step.

---