Blog

Will This Be on the Test? (June 2021)

by Sarah Lonberg-Lew

---

Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

---

Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a high school equivalency test. This month’s question is a short one:

You may recognize this as a one-step problem requiring division… or you may not! There are no division key words in the problem to tip off a student that this is the “right” operation. In fact, the only word in the problem that is a traditional operation key word is “of” and that is usually taken to mean multiply! Even if students solidly know their fraction operation procedures, they will still need to make sense of the context to figure out which operation to do. And if they do manage to settle on division, is it change-keep-flip? Keep-keep-change? Flip-change-keep? Fraction division is not easy to make sense of when all you have is a mnemonic.

Here are some possible approaches that don’t rely on memory tricks:

1. Estimate. Estimation is always a good place to start. Even if an estimate doesn’t give a student enough precision to distinguish between answer choices, the process of making one forces them to slow down and make sense of the problem. You can’t estimate an answer if you don’t understand the question. Students who are accustomed to estimating will be less likely to panic and just do the first operation they think of with whatever numbers they see. In this case, we are looking for the number of laps needed to run four miles. A student might reason that since one lap around the pond was less than one mile, four laps would be less than four miles. That eliminates two answer choices right away! The student might further reason that since one lap was kind of close to one mile, the answer is more than four but probably not twice as much.

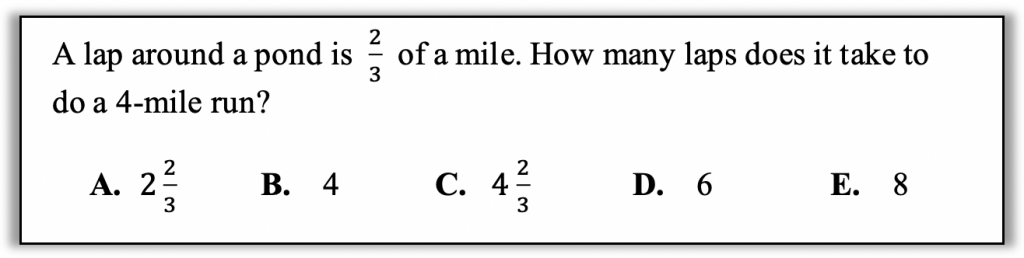
2. “Act” it out. The story in this problem is pretty straightforward. A student taking a test can’t get up and go find a small pond to run around with a pedometer, but they can draw a picture of it, tracing laps around the pond until they’ve “run” four miles. They could use a table to keep track of the total distance like this.

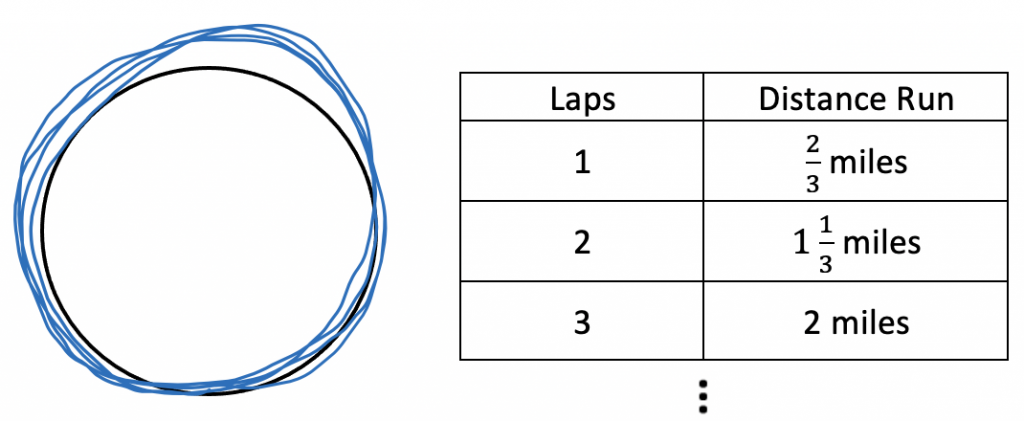
Or they might just keep track of the running total like this:

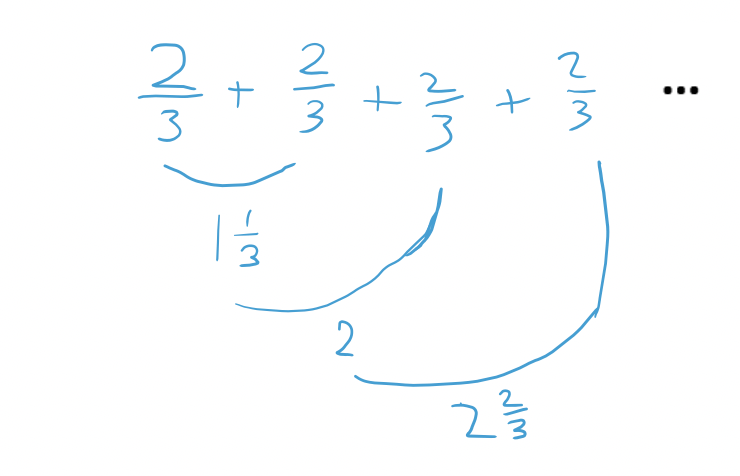
Or they might straighten out the route and keep track of it on a number line:

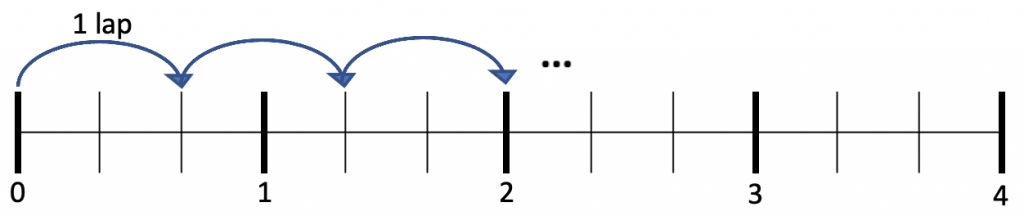
There are many ways to act out the math on paper. (The scribbled drawing of the laps around the pond may not feel necessary to answering the question, and it may not be necessary, but making a sketch can be a good way of entering a problem if you don’t know what else to do. It helps ground your thinking in the context and calm word problem-induced panic.)

3. Reason proportionally. A student who starts “acting out” the situation may get as far as having run 2 miles (3 laps) and realize that she can jump forward. If 2 miles takes 3 laps around the pond, 4 miles should take twice as many since 4 miles is twice as far!

4. Divide using a Singapore strip model (bar model). Wait! Didn’t we say that this was a division problem? So far, none of the strategies have used division at all! Well, all the operations are related and it’s rare to find a question that can only be answered using one operation. In this case, the story lends itself well to arriving at an answer through repeated addition, but it also can be interpreted as a division question: how many groups of ⅔ of a mile are there in 4 miles? With a Singapore strip diagram showing four miles divided into thirds, a student can color and count the groups – every two blocks represents one lap:

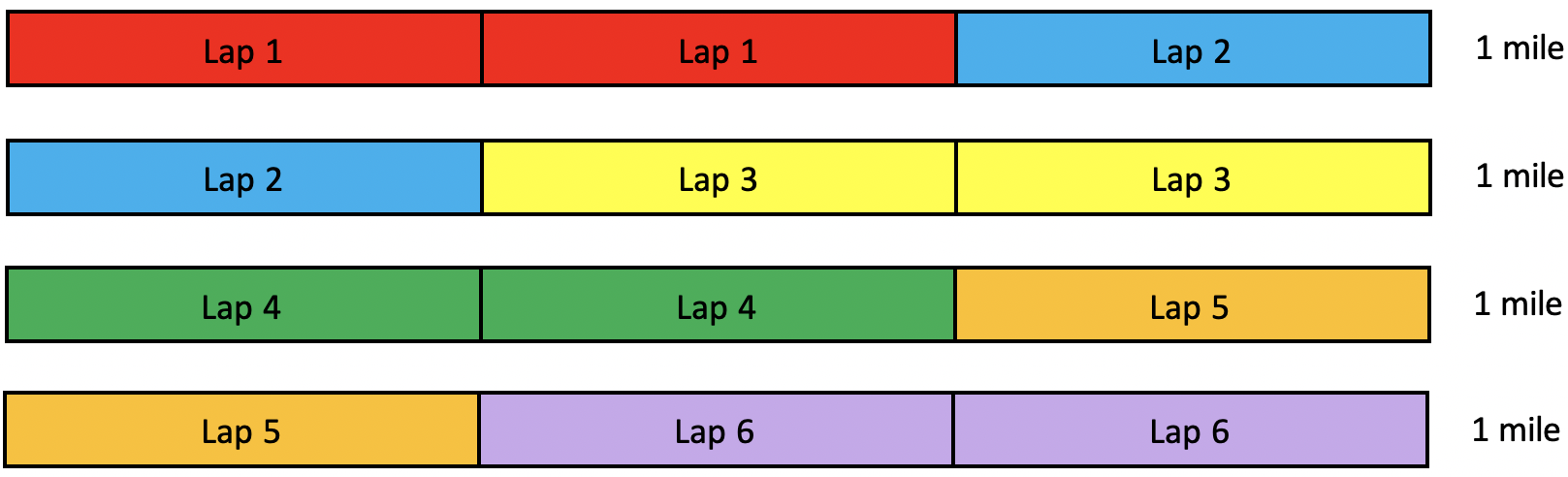
Look back over the possible approaches. What others can you think of? For students who have the confidence to make sense of the problem, to visualize, and to trust their intuition over trying to remember what they are supposed to do, there are many entry points into this task.

---