Will This Be on the Test? (January 2024)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test. Here is this month’s question:
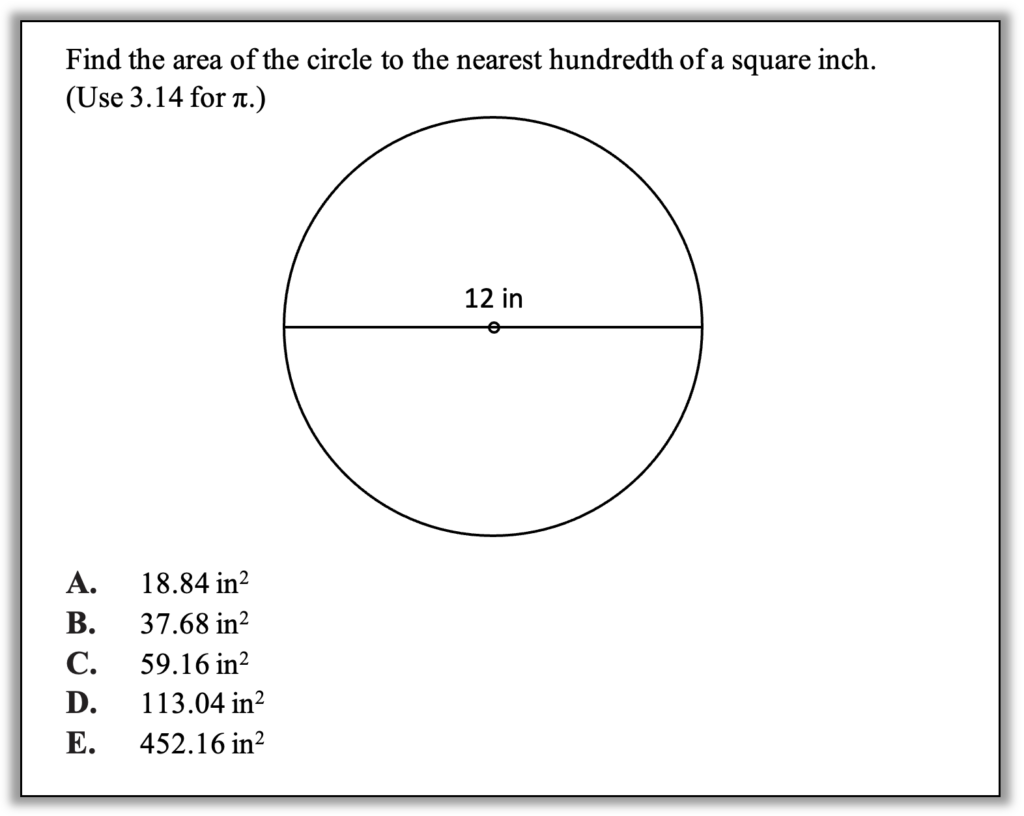

How can you approach this question in a way that makes sense to you? What conceptual understandings or visual tools can you bring to bear? What mathematical concepts do students really need to be able to tackle this problem? How might your real-world experience help you reason about this?
With a question like this, you might think that the only way to solve it is to go to the formula page, then find and apply the right formula. While this is one possible approach, it is also laden with pitfalls for students who do not have the agency or conceptual understanding to make sense of the problem. In fact, every incorrect answer choice in this question results from either applying the wrong formula or misapplying a formula. (As a bonus challenge, you may try to figure out how a student could arrive at the incorrect answers.) When students are focused more on answer-getting than on sense-making, they are prone to grabbing the first formula they see and plugging in the numbers they have.
But what other options are there? In questions of area, on tests and in life, it is often sufficient to be able to make a good estimate (especially because incorrect answer choices are often based on misapplying formulas and not on reasonable estimates). Here are some ways a student who has studied some area concepts could make a good estimate about the area of this circle:
1. Estimate with an outside square. One way to get an estimate of the area of a shape is to calculate the area of a simpler shape that it fits inside. A student might recognize that they can build a square around the circle (like the one below) and the sides of the square will be the same as the diameter of the circle (even if the student hasn’t yet learned the word “diameter”):
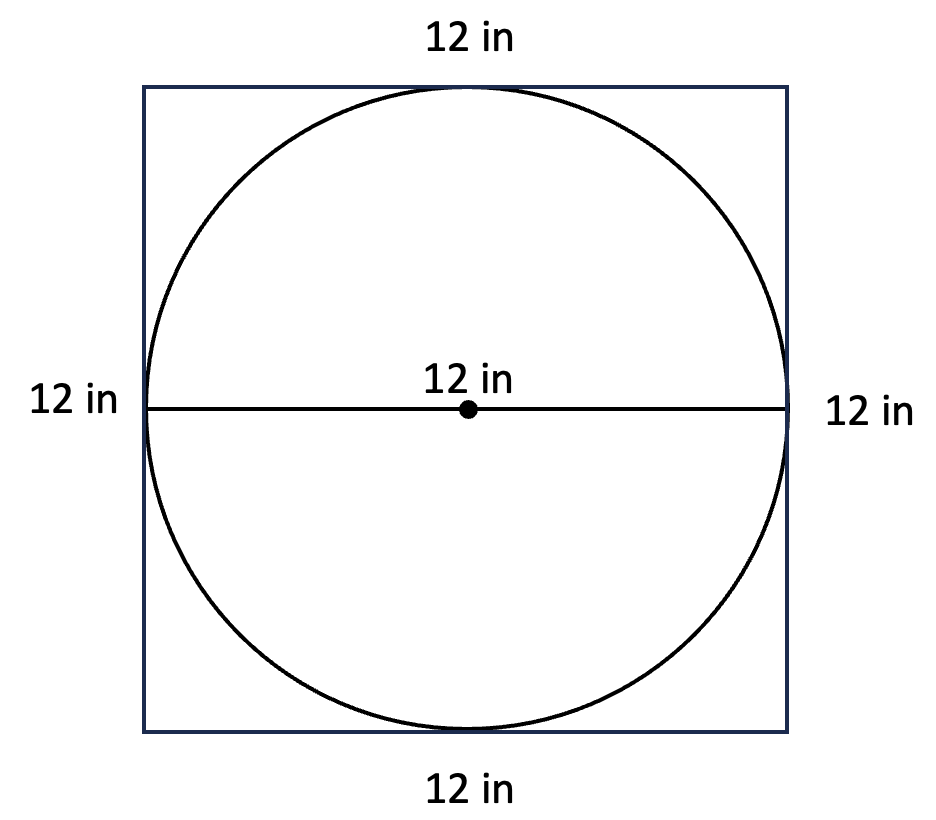
Finding the area of the square will give an upper boundary to the area of the circle. It also could give an idea about what size number would be reasonable. Is the circle a little smaller than the square or a lot more? Is the circle more than half the area of the square or less than half? How many answer choices could you eliminate based on this reasoning?
2.Estimate with four outside squares. Thinking about the radius instead of the diameter, a student might create four shapes that enclose the circle instead of just one, like this:
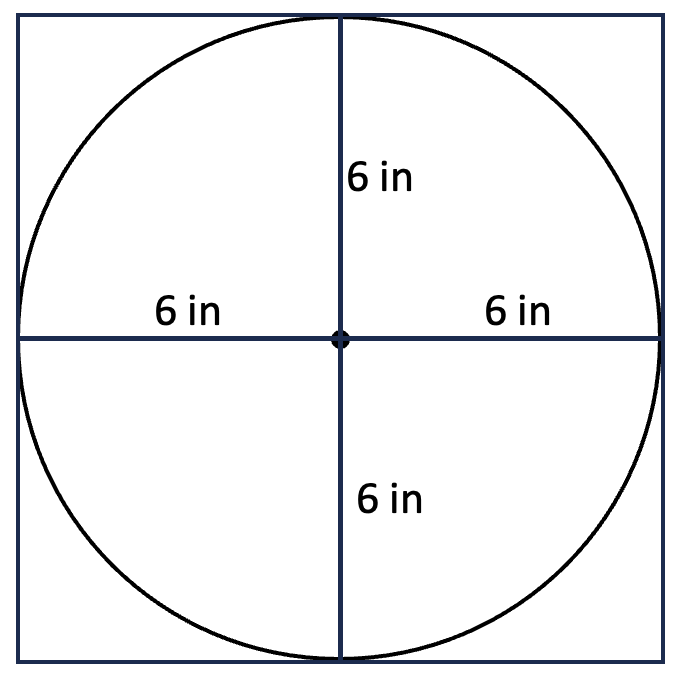
This is a less likely approach because the radius is not given in the original question, but it is one that is worth exploring. Ask yourself: About how many squares built on the radius of the circle would it take to equal the area of the circle? More or less than four? More or less than three? This line of thinking may prove useful when investigating more precise ways of thinking about the area of a circle later on.
3. Estimate with inside triangles. A student might look for a lower boundary to the area of the circle by finding the area of a shape or shapes that fit entirely inside it. For example, a student could draw right triangles inside the circle like this:
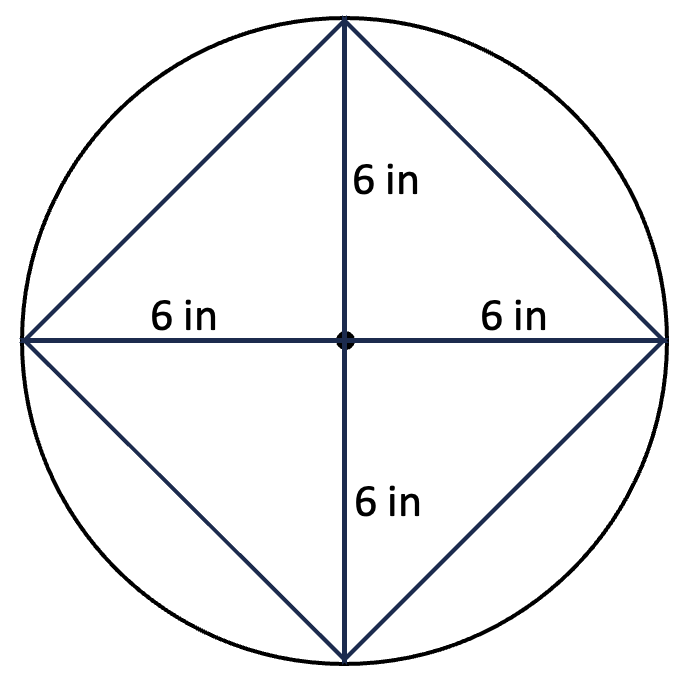
What estimate for the area of the circle will this yield? Which answer choices seem possible or reasonable with this approach?
4. Estimate inside and outside. Putting together information gleaned from estimating with an outside shape and estimating with an inside shape will start to narrow down the range within which the actual area lies. Another approach to get a more accurate estimate is to combine shapes that include some extra area and shapes that leave some area out, like this:
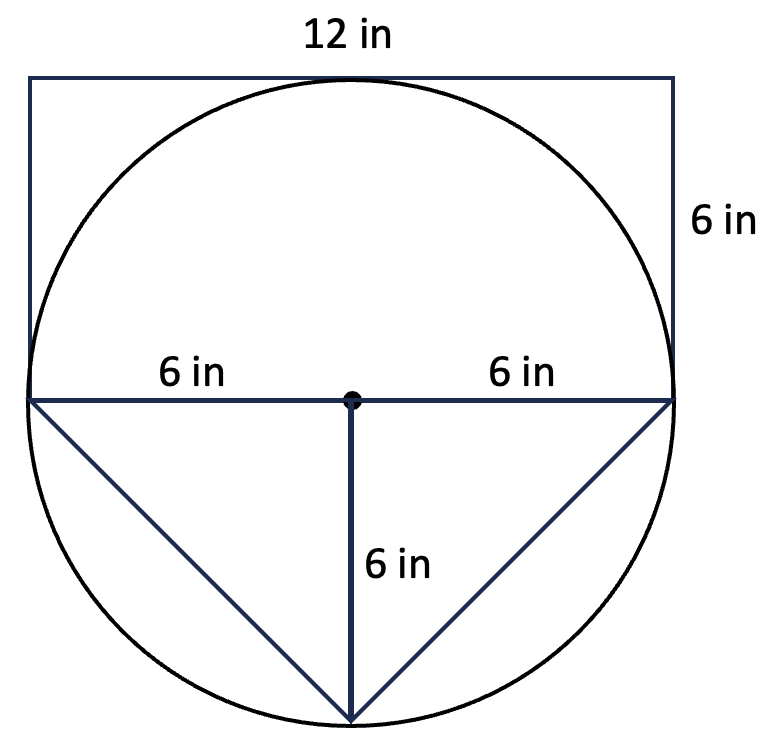
An estimate made with these shapes will be closer to the actual area because the extra area on the top will approximately make up for the cut off area on the bottom. Do you think the estimate will come out over or under the true area of the circle? Or could it be exactly right?
If you are thinking of doing a Test Talk with this question, it would work well at the beginning of a lesson on finding the areas of circles. You may remind students that the formula for finding the area of a circle was not always known. It was discovered by people who experimented with estimation and patterns. (While mathematical discoveries are most often credited to ancient Greeks, we know that mathematicians from Babylon, Egypt, and China also explored this question—and who knows what other peoples’ stories have not been told?) Encourage students to follow in the footsteps of those who made great mathematical discoveries and use what they know about area and about circles to estimate creatively and you will lay a strong foundation for explorations that end in understanding and being able to apply the correct formula.

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
