Will This Be on the Test? (December 2022)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test. Here is this month’s problem:


How can you approach this question in a way that makes sense to you? What conceptual understandings or visual tools can you bring to bear? What mathematical concepts do students really need to be able to tackle this problem? How might your real-world experience help you reason about this?
This is another one of those questions that can cause a student’s brain to shut down simply because it is presented in a test format. Seeing a question in the context of a test or of math class can churn up math anxiety that wouldn’t arise if the student were in the actual situation. Most of us reason about finding the best deal all the time, but when we see something like this on a test page, our thoughts might default to “I can’t remember what I’m supposed to do” rather than to whatever strategies we use comfortably in the real world. Of course, there is a traditional “math class” way to solve this, but there are many other ways to reason beyond a single strategy. Before bringing a question like this to your students, you might ask them to talk generally about how they find the best deal when they are shopping. You may be surprised by the variety and creativity of the strategies they already have!
Here are some possible approaches:
1. Estimate! (Take 1) This is a real-world situation and, in the real world, we often try to get away with doing as little calculation as possible. In many cases, estimation is all we need. In this situation, a student might check out what whole dollar amounts each rate is between. For example, the rate for Pet Supplies Unlimited must be more than $3 per pound because at $3 per pound, 8 pounds would only cost $24. However, that rate must also be less than $4 per pound because at $4 per pound, 8 pounds would cost $32. (So the actual price is between $24 and $32.)
Try filling in the rest of this chart yourself. How does that move you toward finding the answer? Can you get all the way there with estimation? Why or why not?
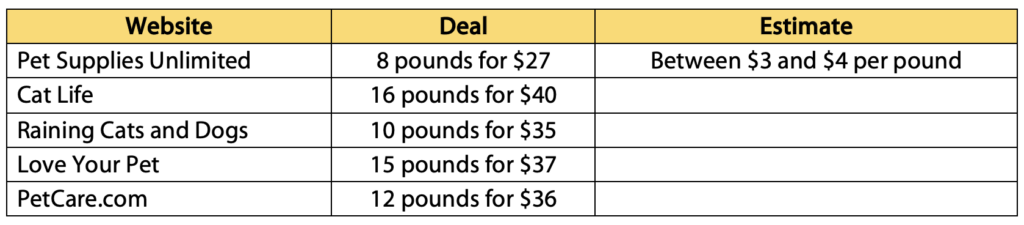
(Even if you have a calculator handy, it’s a good idea to estimate before you calculate. You’ll see why in approach #4.)
2. Estimate! (Take 2) Taking a moment to read through the different deals, a student might notice that the prices for the three brands at the bottom of the table are very close together in price, but the number of pounds for the price differs by at least 2 pounds. At PetCare.com, you can get 2 pounds more than at Raining Cats and Dogs for only $1 more. And at Love Your Pet, you can get 3 pounds more than at PetCare.com for only $1 more. How does this help you think about which of those three brands might be the best deal?
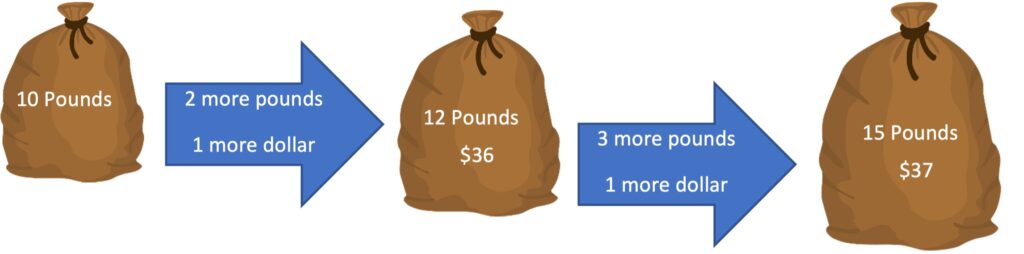
Once you have an idea of which of these three options is the best deal, how can you extend your reasoning to compare that to the Pet Supplies Unlimited and Cat Life prices?
3. Estimate! (Take 3) Another good way to use estimation is by making individual comparisons. For example, at Pet Supplies Unlimited, you can get 8 pounds for $27 and at Cat Life, you can get 16 pounds for $40. Students might notice that the number of pounds in the deal from Cat Life is twice the number of pounds in the offer from Pet Supplies Unlimited. They could compare these deals by doubling the deal from Pet Supplies Unlimited… but do they really need to do that calculation? All they really need to know is whether doubling the deal from Pet Supplies Unlimited will cost more or less than $40.

One individual comparison eliminates one answer choice. What comparison might you make next?
4. Calculate unit rates. Okay, so you want to use your calculator to find the exact price per pound? There’s nothing wrong with that. It can be a quick way to get through a question like this on the test or in reality. But make sure you’ve thought about what you are doing first (maybe by estimating)! We find unit rates by doing division, but which number do we divide by what? Consider the table below:
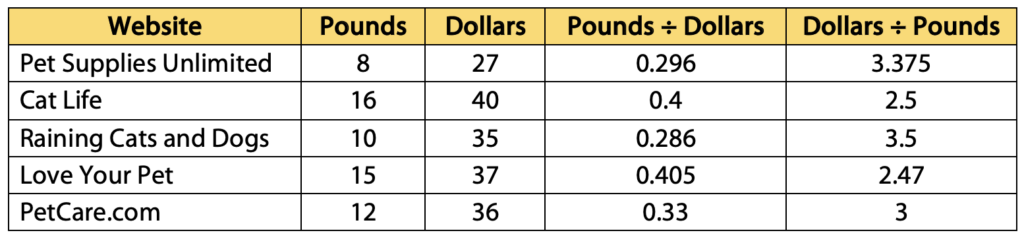
Estimating before calculating will help you know which of the calculations gives the price per pound of kitty litter. But what do the numbers in that other column mean? How could they help you identify the website with the best price? (Hint: If dividing dollars by pounds gives you dollars per pound, what does dividing pounds by dollars give you?) It’s easy to divide in the “wrong” direction if you aren’t paying attention, but knowing what kind of answer is reasonable will help you recover quickly from that misstep.
How would you have figured out the best deal if you were faced with this dilemma in reality? Was your approach discussed above? When it comes to solving real problems with proportional reasoning, there are so many good strategies, and estimation is invaluable. Because questions involving proportional reasoning come up so often in our lives, we may even be estimating and reasoning about them without realizing we are doing math! When we help students prepare to use math more confidently and flexibly in their lives, we are also preparing them to use it confidently and flexibly on the test. Taking time to draw out and celebrate the creative ways that students already reason mathematically will help them break down the imaginary barrier between math that happens in the classroom (and on the test) and math in the real world.

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
