Will This Be on the Test? (April 2024)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test. Here is this month’s question:


How can you approach this question in a way that makes sense to you? What conceptual understandings or visual tools can you bring to bear? What mathematical concepts do students really need to be able to tackle this problem? How might your real-world experience help you reason about this?
I used to teach students that a formula was like a recipe. To follow the formula and produce the answer, they needed to gather all the ingredients and put them together in the way the formula stated. For example, to find the area of a triangle, you use this formula:
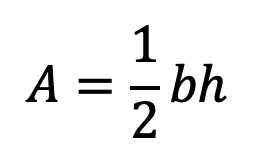
The ingredients in this formula are b and h and the final dish produced is A. The formula tells you what to do with b and h to get A. To find the volume of a sphere, you use this formula:

The main ingredient in this recipe is r, and the formula tells you what to do with r to get V.
But that approach leaves a lot out. This cookie-cutter approach (pardon the pun) only lets you do one thing—start with the ingredients and produce the dish (the answer). That may be good enough in the kitchen, but a test question may ask students to do something more involved. In this test question, the volume is given and the radius is the missing information. One way to approach this problem is to manipulate the formula so that it gives the radius instead of the volume, either before or after plugging in the known information. This strategy works, but it also requires a pretty high level of comfort and fluency when working with equations. Here are some other possible approaches:
1. Estimate with an answer choice. It’s often useful with multiple choice questions to think about what kind of answer would be reasonable. In the case of this question, students might initially think that none of the answer choices seem reasonable—all the possibilities for the radius seem very small compared to the volume. However, students who have spent some time exploring the relationship between the radius and the volume of a sphere will have a much better understanding of why the volume is so much bigger than the radius. Consider what happens when you use the radius of a sphere to find its volume: 1) the radius is cubed (or raised to the third power), 2) that number is multiplied by π (which is a little more than 3), and 3) all of that is multiplied by 4/3, which is bigger than 1 (it’s about 1.33). That is a lot of multiplying. Using the largest answer choice (23.7 inches) as an example, a rough estimate of the volume of a sphere with that size radius could be found by rounding the radius to 24, rounding π to 3, and multiplying (24)(24)(24)(3)(1.33). That comes to 55,157.76 cubic inches. That is over 30 times bigger than the beach ball in the question! It turns out that cubing a number can make it a lot bigger. Students who take time in class to consider the sizes of the numbers involved in their computations will be better equipped to estimate in test situations and in life. (A friend of mine found this out the hard way when they ordered several cubic yards of soil for their garden without considering how big a cubic yard really is. They ended up with a lot more soil than they were expecting!)
2. Estimate with friendly numbers. It might have seemed at first glance that the largest answer choice was the most reasonable, but after estimating with that answer choice, we see that the radius is probably a lot smaller. In the middle of the answer choices, we have two numbers that are close to 10, one a little less and one a little more. A student might do a quick estimate with a radius of 10 inches: (10)(10)(10) = 1,000. Multiply that by 3 and we are already over the target volume without even multiplying in the 1.33. What answer choice might a student investigate next given this information?
3. Use a story table. A potential pitfall in exploring the answer choices through applying the formula for the volume of a sphere is that there are many places where applying a complicated formula can go wrong, especially when using a calculator. It can be easy to press the wrong button, misapply the order of operations, or get an incorrect answer due to not understanding how the calculator applies the order of operations. A story table can help a student make sense of the formula and focus on one calculation at a time. In a story table, the student tells the story of the equation or formula one step at a time, kind of like writing out a recipe step-by-step. Each column of the table, reading from left to right, brings in the next event in the story of the variable. In this case, we are telling the story of r and trying to find a value of r where the end of the story is 1,766. Here’s how a story table for this question could look (using 3.14 for π and 1.33 for 4/3 to make calculator use easier):
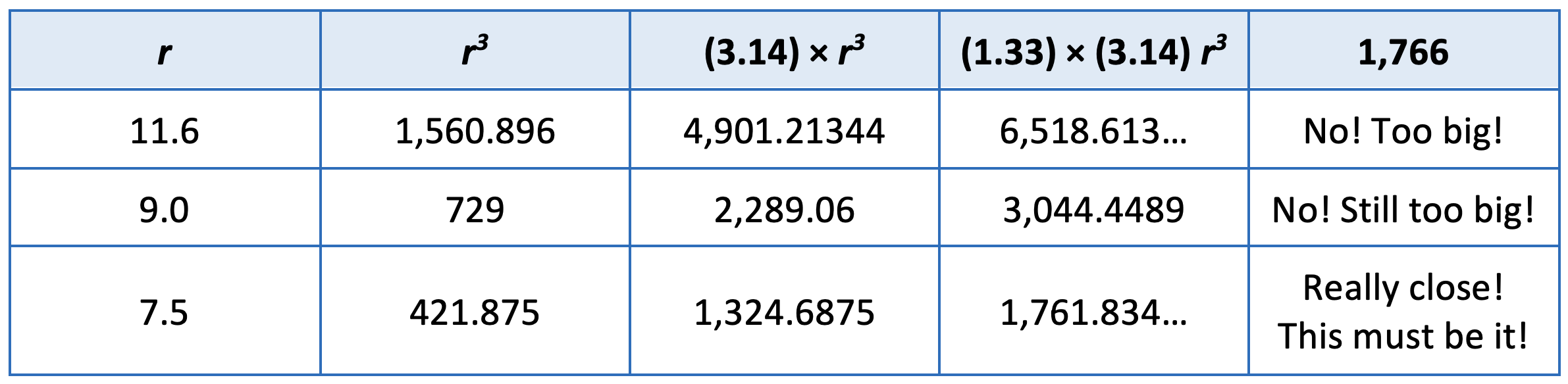
Note that even with the story table, we still don’t get exactly to the given volume. Why do you think that is?
You can learn more about story tables at https://nyccami.org/story-tables/ where there is a write-up of a meeting of the Community of Adult Math Instructors* that was all about using them. They are a great tool for building algebraic reasoning and exploring patterns.
A test question like this may have been written to test students’ ability to rewrite formulas or solve complicated equations, but a big limitation of standardized testing is that the test can only measure whether or not a student got the answer correct—it cannot measure their thinking. And as it is on the test, so it is in the real world: finding a path to a solution is all that matters. It doesn’t have to be a prescribed path or the most efficient path. Consider that even recipes, with lists of specific ingredients and step-by-step instructions, are not the only ways to produce delicious meals. In fact, they may not even be the best way! The best cooks have conceptual understanding of their culinary creations, which allows them the freedom to be creative with their process.
*Interested in checking out a Community of Adult Math Instructors meeting? Visit the CAMI Meeting page!

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
