Will This Be on the Test? (April 2023)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Welcome back to our continuing exploration of how to bring real conceptual reasoning to questions students might encounter on a standardized test. Here is this month’s problem:


How can you approach this question in a way that makes sense to you? What conceptual understandings or visual tools can you bring to bear? What mathematical concepts do students really need to be able to tackle this problem? How might your real-world experience help you reason about this?
This question is challenging not only because of the mathematical content (reasoning about how changes to dimensions affect area), but also because it raises the question of whether there is enough information given. Answer choice (E) is a tempting option because there seems to be some information glaringly missing from the question. How can a student investigate the answer choice options when they are not given the dimensions of the garden to begin with? Students who have learned to circle the important numbers and underline key words in a question may be at a loss because very few numbers are given. So, is it possible to answer this question without being given the dimensions of the garden? How can a student be sure of their answer when they don’t have numbers to work with?
Here are some possible approaches:
1. Collect some data. A student who prefers to work with concrete numbers may choose to work with the only number that is given—the area of Joy’s garden is 30 square feet. That means that whatever Joy does to double the area, the new area must be 60 square feet. A student could make a list of possible dimensions for Joy’s garden before and after the area is doubled and look for a relationship that fits one of the answer choices.
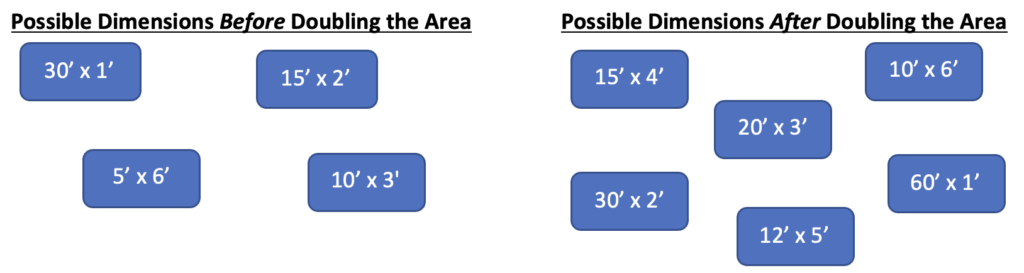
What relationships can you see between the before dimensions and the after dimensions. Do any of them fit the answer choices? Jumping in and collecting some data can help a student get a handle on the question. There may be enough here for them to be able to choose an answer or this line of thinking could lead them to another strategy.
2. Pick dimensions and experiment. Students who are empowered to interrogate test questions and think outside the box may realize that the whichever answer choice is correct has to be correct regardless of the original dimensions of the garden. It is contrary to the math and test-taking training many of us grew up with to think you can just make up information, but a student who has practice with making generalizations will know that some statements can be true regardless of the specific numbers involved. This student may think, “if the correct answer is true for any garden with an area of 30 square feet, it must be true for a garden whose dimensions are 6’ x 5’” and thereby arrive at a concrete place from which to investigate. Starting with a garden whose dimensions are 6’ x 5’, they might then try different answer choices, for example:
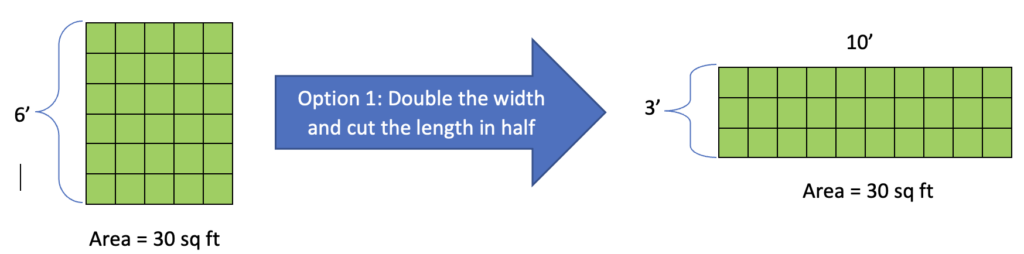
Answer choice (A) did not double the area of the garden. In fact, it did not change it at all! An exciting possible outcome of this approach is that the student might be inspired to investigate whether this always happens when you double one dimension and halve the other. But at least for now, they know that this approach does not double the area of a 30 square foot garden and can move on to try another.
3. Reason visually and generally. A student who is comfortable thinking more abstractly could quickly sketch out the scenarios in the answer choices to get an idea of which ones seem like they would double the area of the garden. For example, a student might be drawn to the idea of doubling both the length and the width (answer choice C) and draw a sketch to investigate it like this:
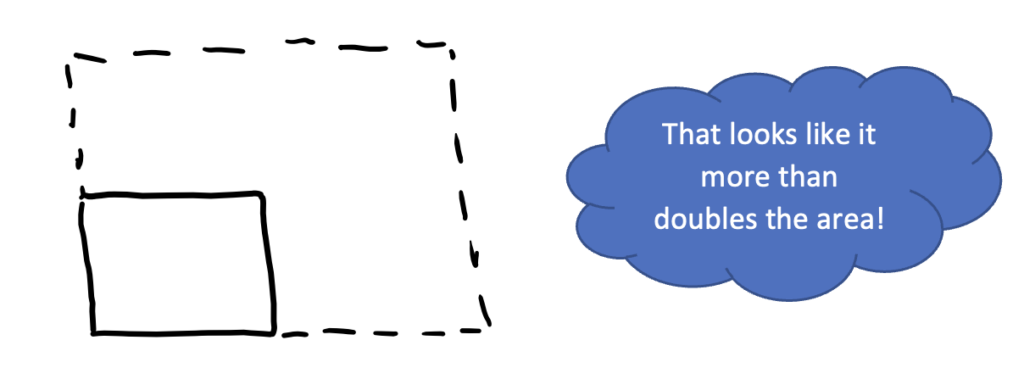
What might it look like to sketch out the other answer choices?
When encountering a question for which a student does not immediately have a clear idea of how to move toward a solution, it can be very tempting to choose an option like option (E) in this question. However, it is often possible to draw mathematical conclusions even when specific information is missing. When interesting relationships or patterns appear (like the area not changing in approach #2 in this column), we should build the habit of asking questions about them—Was this a coincidence? Will this always happen? How can I be sure? Can I find a counterexample? Engaging regularly in this kind of thinking will prepare students to decide whether they need more information or whether they can make generalizations.

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
