Will This Be on the Test? (March 2021)
by Sarah Lonberg-Lew
Welcome to the latest installment of our monthly series, “Will This Be on the Test?” (You can find earlier installments as you scroll down the blog.) Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.
Last month we looked at a question about a snail crossing a garden. Modeling the question with number lines or Singapore strips made it very accessible. (If you haven’t read that column yet, I recommend you do so before continuing with this one.) What if the fractions involved in the question were a little less friendly? Would the same visuals and conceptual strategies still work? This month I invite you to challenge yourself to solve a slightly thornier variation using visuals and conceptual understanding.
Here is this month’s challenge. The snail is back, but the numbers have changed.


Before you read further, allow yourself to bring your full mathematical reasoning power to bear on this challenge. How many strategies can you think of? What visuals could you use to help you solve this? Also ask yourself, what skills and understandings do students really need to be able to answer this?
Here are some possible approaches:
1.Estimate! The snail has been traveling for 2/3 of an hour (or 40 minutes) already and is only going to travel for another 10 minutes. Drawing a quick sketch can help a student think about how much farther it looks like the snail would get. About how far do you think the snail would get in 10 more minutes?

The snail is already just over halfway across the garden, so answer choice (c) can be eliminated because it is less than half. Answer choice (a) is more than half, but not by much. From the sketch, it looks like the snail will be well past the halfway point in another ten minutes, so answer choice (a) is not likely. Answer choice (b) is more than one, and it doesn’t look like the snail is going to make it past the end of the garden in only more 10 minutes. There are still a couple of possible answers left. Which one would you choose just from eyeballing the picture? What fraction understandings were used here?
2.Use a Singapore strip diagram (also called a bar model or tape diagram). A student might start with a bar representing the 4/7 of the garden the snail has already crossed. Notice that it bears a resemblance to the sketch above; both show 4/7.
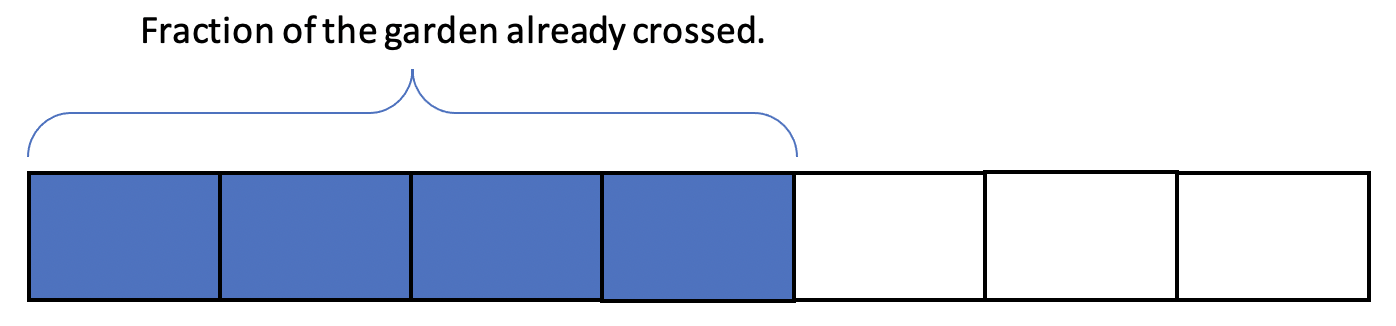
This is where it gets a little trickier. The snail traversed those four blocks in 2/3 of an hour. A student who understands that unit fractions (fractions whose numerator is 1) are single pieces and non-unit fractions are groups of pieces may reason that those four blocks are covered in two chunks of time that are each 1/3 of an hour. In other words, the snail covers two blocks every 1/3 of an hour, or every 20 minutes.
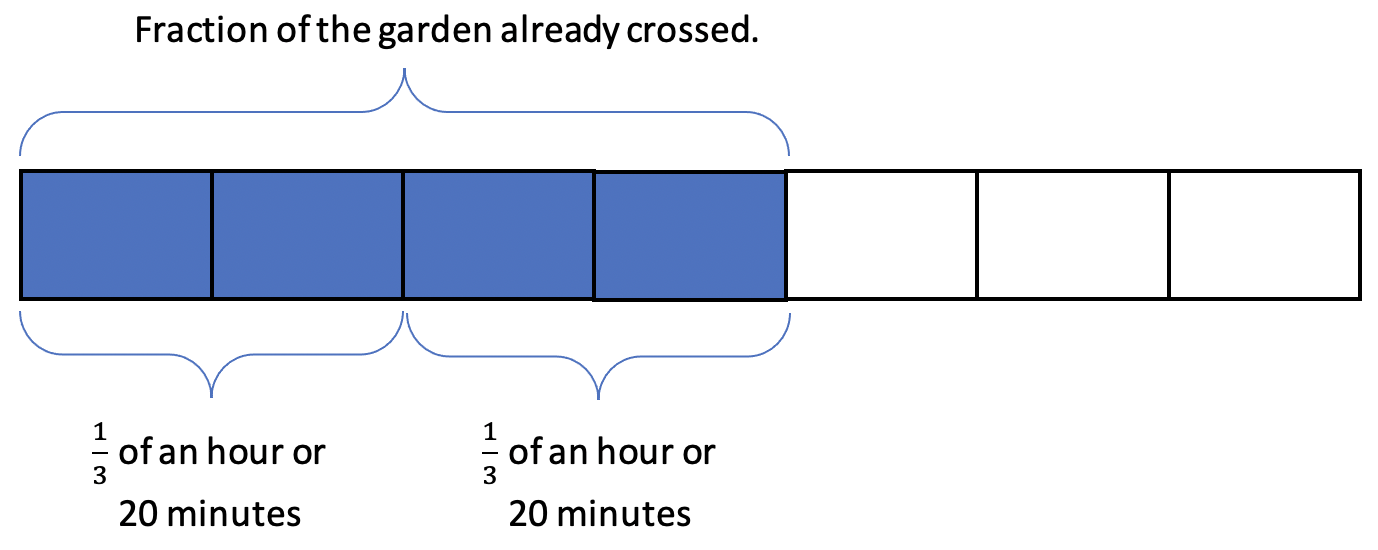
If we know how many more blocks the snail will travel in 20 minutes, how many blocks will it cover in another 10 minutes? What total fraction will that make? (The diagram above doesn’t show the final step of adding on the last 10 minutes of travel.)
3.Reason proportionally. This task is about something moving at a constant rate. In other words, the distance the snail covers is proportional to the amount of time it has been traveling. A student might reason that the 10 minutes the snail has yet to travel is one-fourth of the 40 minutes it has traveled so far, so the snail would cross an additional fourth of the distance it had already covered. Thinking about finding 1/4 of 4/7 of a garden might make your head spin, but looking at the picture of 4/7 represented as four blocks out of seven makes it easier to see that 1/4 of 4/7 is one block.
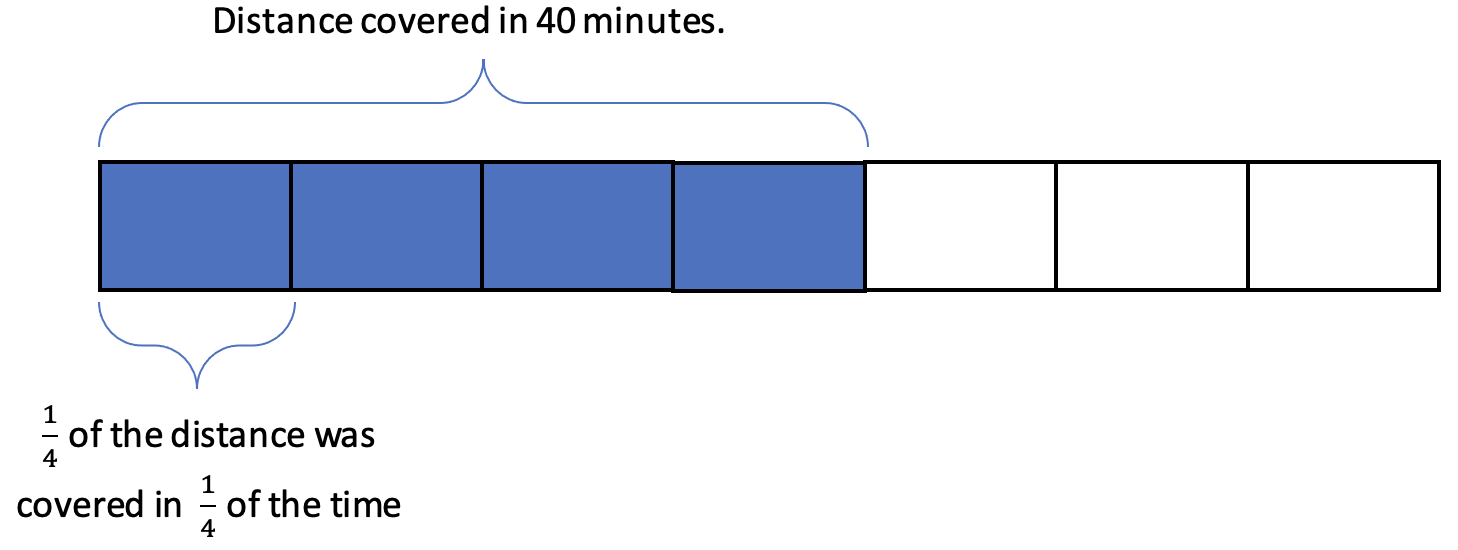
Once again, we found that visual and conceptual approaches carried us through without ever needing to “choose and apply an operation.”
This question of course can also be answered using fraction operations, but it takes a few steps. First, divide the distance covered by the time it took to cover it to get the rate: 4/7 ÷ 2/3 = 6/7 of the garden per hour. Then, multiply the rate per hour by the fraction of an hour the snail adds onto its journey (10 minutes). Ten minutes is 1/6 of an hour so 6/7 x 1/6 = 1/7 more of the garden that would be covered in the extra time. Finally, to determine the total amount of garden covered, add the new distance to the original distance: 4/7 + 1/7 = 5/7, which is answer choice (d). That was three operations and not a very intuitive path through them. (It’s also not the only possible operations approach.)
Even though the operations approach is valid, it tends to elicit the I’m-never-going-to-remember-all-these-steps! response from students. Having to do three different fraction operations to get to the answer can make a student want to run the other way. On the other hand, giving students visual and conceptual tools prepares them to chart their own path through problems in a way that makes sense to them.

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
