Will This Be on the Test? (January 2021)
by Sarah Lonberg-Lew
Welcome to the first installment in 2021 of our monthly series, “Will This Be on the Test?” Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually. (You can find earlier installments as you scroll down the blog.)
I learned a lot of rules in math class, and when I started teaching math, I taught a lot of rules. It was easier to teach students to memorize the rules rather than help them fully understand the concepts (especially when I didn’t always understand the concepts myself). When I taught math to high schoolers, I remember teaching a chapter on the rules of exponents. There was a separate section of the chapter for each rule and I taught them one at a time, so that students could memorize and practice applying each rule before moving on to the next. We spent at least a week on that chapter, covering a new section each day. For some reason, though, everything always fell apart in the last section of the chapter where the problem types were all mixed together and students had to figure out which rule to apply or sometimes whether to apply more than one rule.
There was a time in my teaching career when, if a student had asked me about the problem below, I would have said, “You have to know the rules to be able to solve this.” I don’t say that anymore. How about you? Could you figure out a way to approach this without knowing “the rules”?

Before you read further, take a few minutes to challenge yourself to come up with more than one way to approach this task. How many strategies can you think of? What visuals could you use to help you solve this? Also ask yourself, what skills and understandings do students really need to be able to answer this?
Before we get into some different approaches, let me be clear that if students do not have a grasp on the idea that a letter can stand for a number, then this problem is most likely out of reach and they should not spend time on it. However, if a student has that concept and knows what an exponent means, they do not have to have memorized a set of rules to be able to reason through this. (And while letters representing numbers is an abstract concept, it is an understanding that students can begin building early on.) Here are some possible approaches.
1.Try it with a number. Just because the problem is written with variables doesn’t mean it has to be solved that way. One important understanding about equivalent expressions is that they will have the same value no matter what the value of the variable is. This means that a student can change x to a friendly number, like 2, and work out a problem like the one in our example:
24 • 25
16 • 32
512
Now the student only needs to figure out which answer choice has a value of 512 when x = 2.
Note: Even with a small number like 2, the value of the expression is going to be pretty big, so students might want to use a calculator. Choosing 1 is not a good idea. Why is that? Could your students see why?
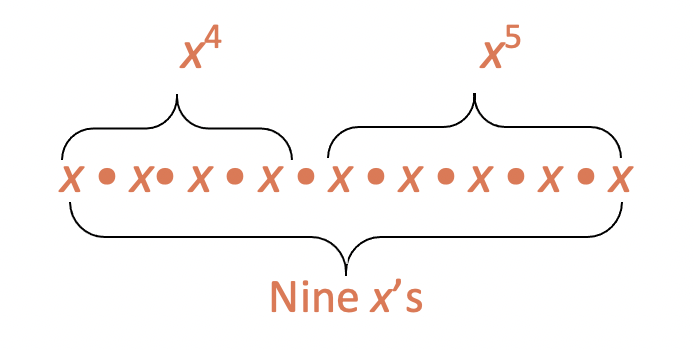
2.Write it out the long way. A student who knows the meaning of an exponent can write equivalent expressions to x4 and x5
like this:
x4 = x • x • x • x
and
x5 = x • x • x • x • x
The student can now multiply the longer expressions together like this:
Now the student can turn their answer back into an exponential expression to match one of the answer choices.
3. Figure out the rule on the fly. One of the most powerful tools in a mathematician’s toolbox is being able to figure out how complicated things work by thinking about simpler things. A student who is empowered to think of themself as a mathematician may realize that they have the power to discover or recreate the rule by looking at simpler cases. A student might do a few quick experiments with expressions similar to the one in the problem to find out what is going on:
23 • 22 = 2 • 2 • 2 • 2 • 2 = 25 (Check by hand or with a calculator – that works!)
23 • 23 = 2 • 2 • 2 • 2 • 2 • 2 = 26 (Check by hand or with a calculator – that works, too!)
Hmmm… the exponents tell me how many 2s will be in the long expression. It looks like adding the exponents gives me the total number of 2s, so I can add the exponents to get the final exponent.
The rules in math were not made up by some high mathematical council that decided one day to confuse generations of students by making the rule that when you multiply expressions with exponents you add the exponents. You add the exponents because it makes sense to do so when you understand how exponents work. The reason that students jumble up the rules or misapply them is that rules are abstract concepts and abstract concepts must be understood, not memorized, to be useful to students. Teaching rules without reason, especially when those rules are not what you might guess at first, disempowers students because they just have to accept what they are told even if it doesn’t make sense to them. Teaching that rules are formalizations of reasoning and patterns empowers students to discover rules and even solve problems without them — and they are freed from the burden of relying solely on memorization.