Blog

Will This Be on the Test? (October 2020)

by Sarah Lonberg-Lew

Welcome to the second installment of our new monthly series, “Will This Be on the Test?” (If you missed the first blog, check it out here.) Each month, we’ll feature a new question similar to something adult learners might see on a high school equivalency test and a discussion of how one might go about tackling the problem conceptually.

There’s almost always more than one way to tackle a math problem. When teachers encourage students to try out different approaches, students gain confidence in thinking flexibly, experimenting, and finding strategies and solutions that make sense to them.

What about you? How would you approach this month’s problem?

1. They might rely on real world experience to estimate a solution to this. Students who has experience with landscaping, yard work, flooring, tile, etc., may have an intuitive understanding of about how big this backyard is and about how many square feet of sod it would take to cover it. It is important to connect the math that students learn in the classroom to the math they encounter in the real world. Without this connection, students may come to see “school math” as something separate from their lived experience. They may not realize that they can apply what they already know in a testing situation. Students who do not make this connection can end up panicking over trying to remember a formula instead of using their own mathematical intuition.

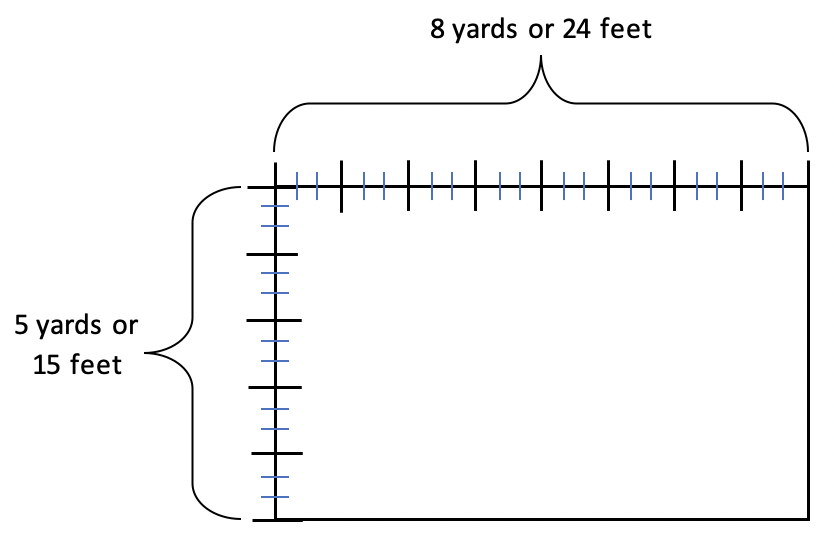
2. If the student has some understanding of the relationship between feet and yards, they might start by drawing a picture of the backyard with the dimensions shown in yards, and then divide each yard into feet to see that they should multiply 15 by 24 to find the number of square feet. 

3. A student might start by drawing a picture of the backyard with the dimensions marked in yards and then figure out how many square feet are in a square yard. Once again, if the student knows how many feet are in a yard, she could use this knowledge to visually divide a square yard into nine equal parts of one square foot each. She might then convert the area of the backyard from square yards (40) to square feet by multiplying 40 x 9. Alternatively, she might calculate total square feet in another way, like finding how many square feet are in each column and then adding all the columns together.

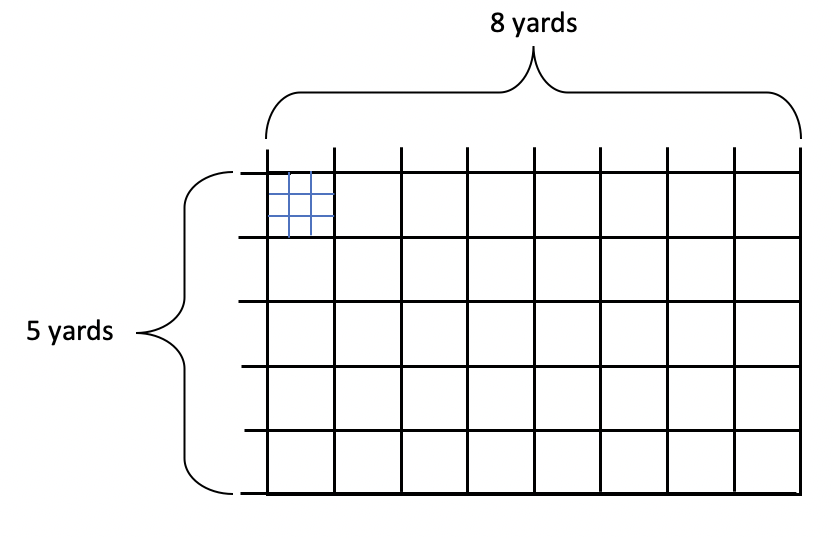
An important point here — even people who are experienced with working with linear and square measures (like feet vs. square feet) can confuse the conversions sometimes. It’s hard to remember to use a factor of 9 when converting between square feet and square yards, but to use a factor of 3 when converting between feet and yards. It’s especially tough in a high-pressure situation like a test. It’s also easy to overlook the conversion completely and quickly answer the question using the wrong unit. This is why it’s so valuable for students to have the confidence to take the time to make sense of a question instead of trying to rely on their memory of what they are supposed to do. Students who draw pictures and rely on their own reasoning are better able to bring their full mathematical power to bear on any question.

What can go wrong?

In contrast to students who confidently take time to draw pictures, consider strategies, or draw on their own experience, there are other students who are desperate to get through the questions. These students may resort to “number grabbing”, or quickly taking some or all of the numbers from a test item and arbitrarily applying to them the first formula they can think of. If they arrive at an answer choice, they pick it and move on. For students without strong conceptual knowledge of math operations, having answer choices can be a pitfall. The developers of standardized tests do not create the wrong answers for multiple choice questions at random; they choose “attractive distractors” — answer choices that will result from number grabbing or not thinking the problem through thoroughly. For example, in our problem above, a student might quickly choose to add or multiply the two numbers given in the problem and arrive, incorrectly, at answer choice A or B without really thinking at all.

Number grabbing is a panic response. For teachers, the best way to help students combat that panic is to nurture their confidence in their understanding, creativity, and flexible thinking. Students who are empowered to approach problems in ways that make sense to them instead of trying to remember how they are ‘supposed to do it’ are much better prepared to make use of all of their skills and abilities in testing situations and elsewhere. When students develop the confidence to think critically and calmly about test questions, they will also have the confidence to do so when they encounter math in real life.

---