What if…?
by Pam Meader

Recently, my grandsons visited me and one of their requests when they visit is to watch a cartoon show called Stinky and Dirty. If you haven’t listened to the show, each episode revolves around a problem that Stinky (the garbage truck) and Dirty (the bulldozer) must solve. I kept hearing, “What if…” throughout the 30 minute show as Dirty proposes a solution and they experiment to see if it works. If not, another “What if…” appears. It’s a cute show, but more importantly, it illustrates a concept we hope we are preparing our students to embrace; one of pursuing problems, examining possible solutions, and trying again if one solution doesn’t solve the problem.
This past week, I listened to two webinars that had similar connections. One was on “Teaching for Biliteracy” and the other was entitled “Knowing and Using Math”. The latter title intrigued me, as I have often used the phrase “knowing math is doing math” (taken from the National Council of Teachers of Mathematics’ work in the late 90s). The facilitator, Jay Meadows from Exemplar, shared that our students live in a world with tons of answers, some of which are false. If all we value are the answers, how are we helping our students?
Many teachers, myself included, thought we had to teach the basics; to practice and practice and then maybe look at a few problems at the end of the chapter. What Meadows and many researchers contend is that we need to do the reverse: start out with a problem of interest, and set about to explore ways to solve it. While some foundation is necessary to do this exploration, even learning basic math facts can take on more exploratory aspects. For example, area models can be created to find facts that have an answer of 24, or we can investigate how many ways to reach the sum of 10.
Brain research backs up the value of exploration. There are four areas of the brain where learning math happens:
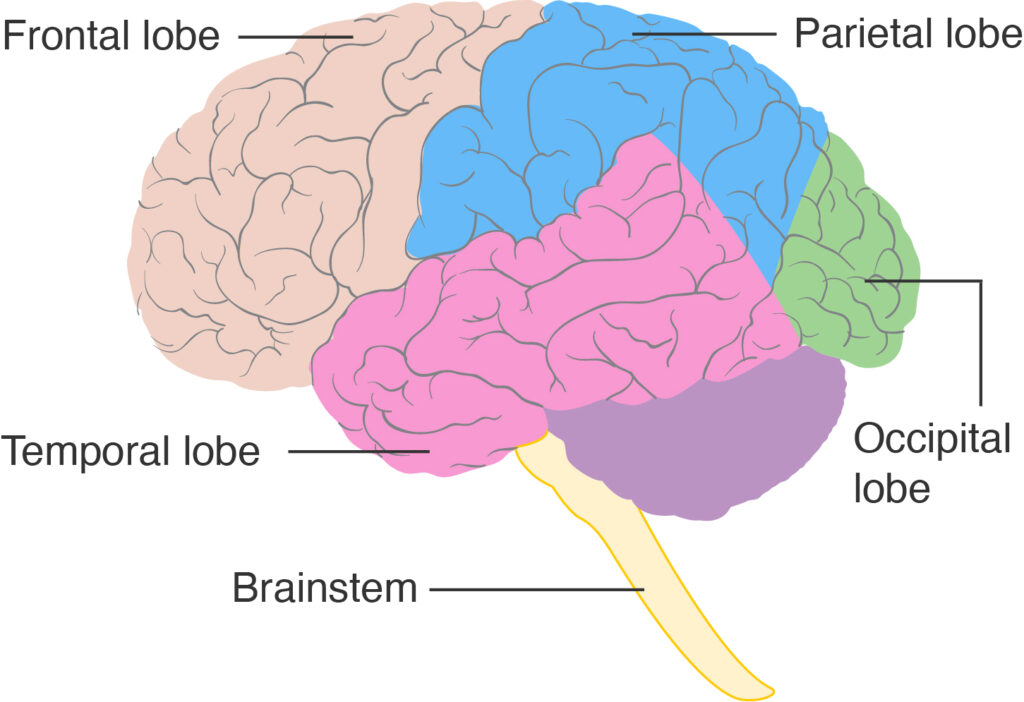
- the frontal lobe deals with problem solving and reasoning;
- the parietal lobe is where number sense, estimation, mental arithmetic, and abstract conceptualization occurs;
- the occipital lobe is utilized for visualization and representation; and lastly,
- the temporal lobe is involved with words and language.
When we teach, we want concepts to “stick”, but how we have been teaching has not worked. If we just tell students how to do something and have them practice the skill until it is mastered, we get short term results. Let’s take fractions as an example. You may have taught fractions over and over again only to have to do it over again the next time you see your students. Why does this happen?
When a person is just shown how to do something, the only part of the brain activated is the temporal lobe, where words and language reside. For concepts to be cemented, teachers need to activate all four areas of the brain. This helps the brain to start to make connections and pathways crisscrossing the regions, or in the words of Meadows, “Exploration provides the stickiness to learn the algorithms.”
As I listened to him, I thought about the algebra class where I began to change my practice. I had attended a conference where a teacher shared some inquiry math projects and I decided to explore this with my students. While I had been teaching algebra in a more hands-on and exploratory way, I still was assigning the pages of “sameness” for practice and sprinkling in a few word problems. I approached this inquiry project as an “add on” for students to complete for the final grade. They were to explore something of interest to them where they could apply their algebra skills to solve their query. I wasn’t sure how this was all going to turn out and worried that it would take too much time. Fortunately, it was the highlight of the course! I was blown away by the projects the students shared. One man was thinking of starting a painting business and explored what he would charge for particular painting projects. He worked with tables and graphs to make his decision. One woman was interested in exercise and weight loss and collected data on her exercise regimen and graphed her results. Yes, it took some time, but I would contend more learning happened in those presentations then any time lost doing kill-and-drill exercises. The students were motivated and energized. The “what ifs” pushed them to explore more.
What if we tried this approach as teachers? What if we presented a problem at the beginning of a class and left it unanswered for days or even weeks? Back in the 90s I participated in a Marilyn Burns week-long session where we did just that. A problem would be presented and we would grapple with it the whole week, changing what we thought was the “answer”, listening to others offer their suggestions, and sometimes never arriving at a final answer. The result? We kept exploring, and opening new pathways of exploration. I can still remember some of the problems we pursued to this day. How do you use math that is productive? Challenge your students to come up with their own questions. Still hesitant or unconvinced? Watch this video for more affirmation (and a fun blast from the past):
References
Jay Meadows, “Show, Solve, Explain: What’s the Difference Between Doing Math and Using Math” Edweb, November 28, 2022. https://home.edweb.net/webinar/math20221128/

Pam Meader, former high school math teacher and proud grandma, taught math in adult education for over 25 years. She is a senior professional development specialist for TERC’s Adult Numeracy Center. Most recently, she helped co-develop Adults Reaching Algebra Readiness (AR)2 with Donna Curry. She is a national trainer for LINCS and Adult Numeracy Instruction (ANI). Pam enjoys sharing techniques for teaching math conceptually, from basic math through algebra, and is co-author of the Hands On Math series for Walch Publishing in Portland, Maine.
