Using Desmos: How Can It Fit in My Classroom?
by Connie Rivera
I was sold on the idea of using free Desmos Classroom Activities as soon as I tried one myself. Why? Because I discovered math ideas I didn’t already know just by working through an activity!
Using tech tools in class can’t be technology for technology’s sake. Our instruction must be focused on the mathematical understandings we want students to develop. Only then should we search for the activities that help students discover those ideas. Desmos is a great source for facilitating deeper understanding of math concepts. Below is a way I’ve helped students develop a concept, beginning with paper and ending with Desmos.
Triangles and Rectangles
First, I started with this printable activity which is an exploration of the relationship between Triangles and Rectangles.
Here are some ideas students develop from Triangles and Rectangles:
- Parts of a fraction must take up the same amount of space, but they might not begin as the same shape.
- If I can prove an area is half of a shape, the other parts must total half the area.
- I can flip and rotate images in my mind to consider a fit.
- For a triangle to be half the area of a rectangle it’s within, it must share at least one side (base) with the rectangle.
In a broader sense, these realizations are about noticing a pattern, generalizing an idea, and visualizing.
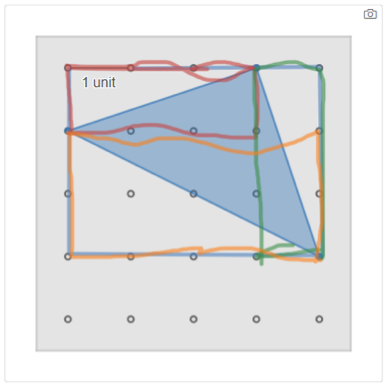
Desmos Classroom Activity: Exploring Triangle Area with Geoboards
Next, I used Exploring Triangle Area with Geoboards with my students. Here are some step-by-step thoughts.
Follow the link above and find the blue “Student Preview” button in the “Screens” section. In order to experience the activity the way your students would, use the at the bottom of the screen to close the “Teacher Moves” and “Sample Responses” the first time through. In fact, try working through the activity yourself before continuing to read this article.
Screen 1: Find the Area #1 Here are two examples of how students used the sketch tool to work through their reasoning.
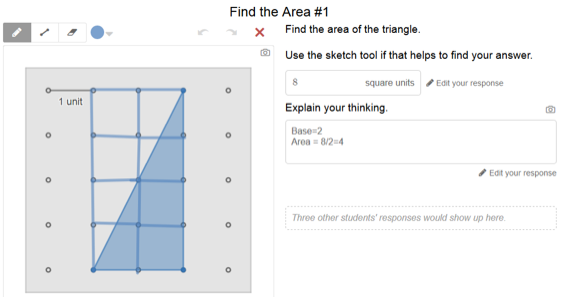
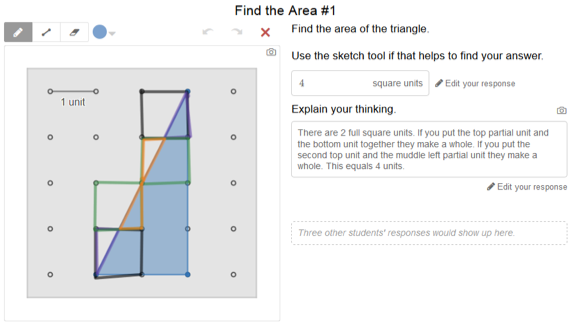
As you can see from the screenshots, other students’ responses would show up on the screen as well — a feature that allows students to see other students’ thinking whether or not they are on the computer at the same time! Knowing that there’s an audience encourages students think about their answers more carefully beforehand. Afterwards, they can consider the accuracy of their answers and edit their responses if need be.
Screen 2: Find the Area #2 The problem on Screen 2 reminds some students of the triangle that didn’t work in the initial Triangles and Rectangles activity, leaving them to find new approaches. In this activity, we can see how the ideas that were beginning to develop in Triangles and Rectangles are explored from a different perspective and extended using Desmos.
In the examples below, we can see in the image on the left that the first student drew a square that encompassed her triangle and found its area (12). Then she marked smaller rectangles and found the areas of the white spaces (1.5, 1.5, 4). Lastly she subtracted the total of the white spaces from the rectangle’s area (resulting in 5 square units).
The second student (the same student from example 2 in Find the Area #1) was, to my surprise, able to carry her visualization process through to this more challenging problem. She complained there weren’t enough colors to show her work, but her explanation made it clear that she could see each piece rotating, flipping, and moving to a new spot to create a square unit. She was surprised that everyone couldn’t see things she saw easily.
It benefits students to hear different ways that other students think through a problem. Finding an efficient solution method doesn’t result in the same solution method for everyone; it gives everyone a chance to find something that works for them.
Here you could pause the class (a feature for teachers in the dashboard) and ask students to share answers to the question, “When you were stuck, what idea got you unstuck?” Some responses might be:
- I can flip and rotate images in my mind to consider a fit.
- I can find the area of a rectangle holding the triangle, and subtract out the area of the outside pieces that I’m able to find the area of. This leaves only the area of the triangle I didn’t know (and now know).
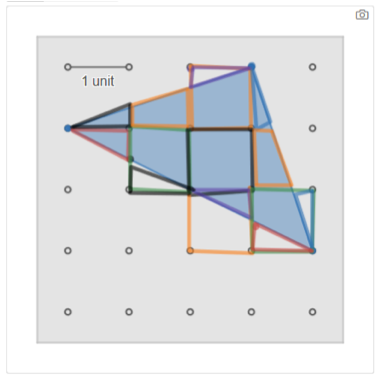
Screens 3 & 4: Create a Triangle and Class Gallery 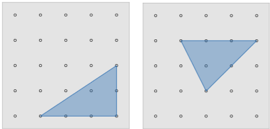 Screen 3 gives students a chance to create new problems of their own to challenge their classmates (and practice what they are learning from a different perspective). Screen 4 is space where students try out their classmates’ challenges. As a bonus, they can also see how others in their class have attempted to solve the same problem.
Screen 3 gives students a chance to create new problems of their own to challenge their classmates (and practice what they are learning from a different perspective). Screen 4 is space where students try out their classmates’ challenges. As a bonus, they can also see how others in their class have attempted to solve the same problem.
Getting Started with Desmos
Are you interested in using this activity with your students? Here’s how to get started.
You can “Create an Account” using the green button on the top right. Next, click the green “Create Class Code” button on the teacher page of this activity. Now you have opened a class. Click “view dashboard”. Your code and how to get there is the first thing to pop up. Share your code with friends to try it out and learn how the dashboard can help you monitor a class.

Connie Rivera teaches numeracy skills to adults of various skill levels, including court involved youth and English Language Learners. She is also a math consultant, providing math strategies and support to programs implementing the College and Career Readiness Standards for Adult Education (CCRSAE) in Connecticut and Massachusetts. As a consultant for the SABES numeracy team, Connie facilitates trainings and guides teachers in curriculum development. Connie is a past President of the Adult Numeracy Network, the adult affiliate of the National Council of Teachers of Mathematics (NCTM), and is a LINCS national trainer for math and numeracy.