Procedural Fluency
by Aren Lew
Procedural fluency, one of the three components of rigor (College and Career Readiness Standards for Adult Education, p. 45), often calls to mind the need for worksheets with the same kind of problem repeated over and over, or software that generates problems for students until they can get five right in a row. It carries an idea that students should practice procedures until they can be done automatically – without thinking – until it is no longer difficult to remember which step comes next.
It is possible for most people to achieve this level of automaticity with any procedure if they practice it for long enough, but there are some major pitfalls to this approach.
Memorization can be a touchy process – start doing something wrong and you may end up memorizing an incorrect procedure and having to work even harder to fix it. (My young nephew, when learning to count, forgot 12 often enough that he memorized the counting numbers without it and had to work hard to learn it.)
Also, there is truth to “use it or lose it.” If you get out of practice with a procedure you’ve memorized, you may have to memorize it all over again, taking almost as much time as you did the first time.
Another major pitfall to only memorizing steps is that if you forget or misremember just one step, the entire procedure will not work, and you may not even realize you’ve made a mistake.
Luckily, memorizing steps is not the only way to achieve fluency with procedures. Fluency can also be achieved by gaining conceptual understanding and practicing reasoning. Here’s an example of how a student might achieve fluency with multiplying two-digit numbers through understanding and practice:
1) The student engages with hands-on, conceptual activities in class. Through working first with arrays and later with area models, the student has several Aha! moments. (This takes place over several classes.)
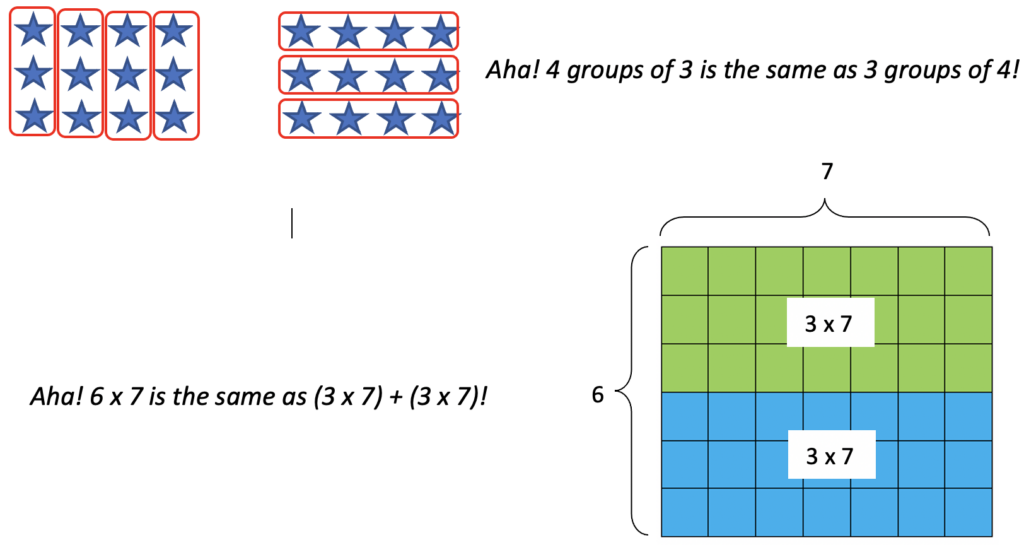
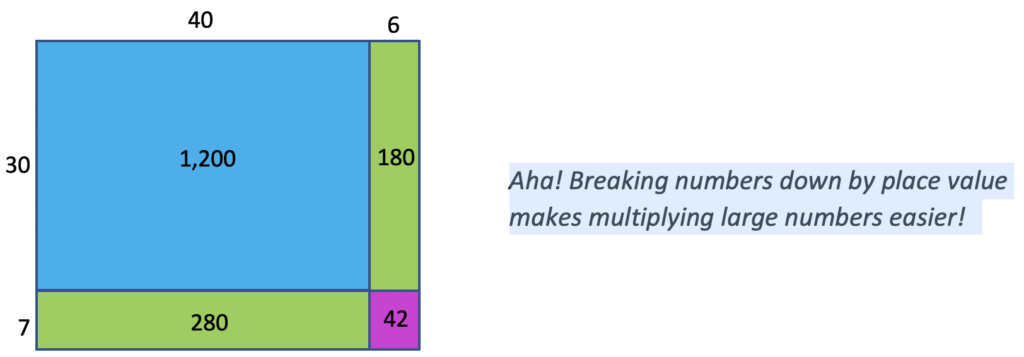
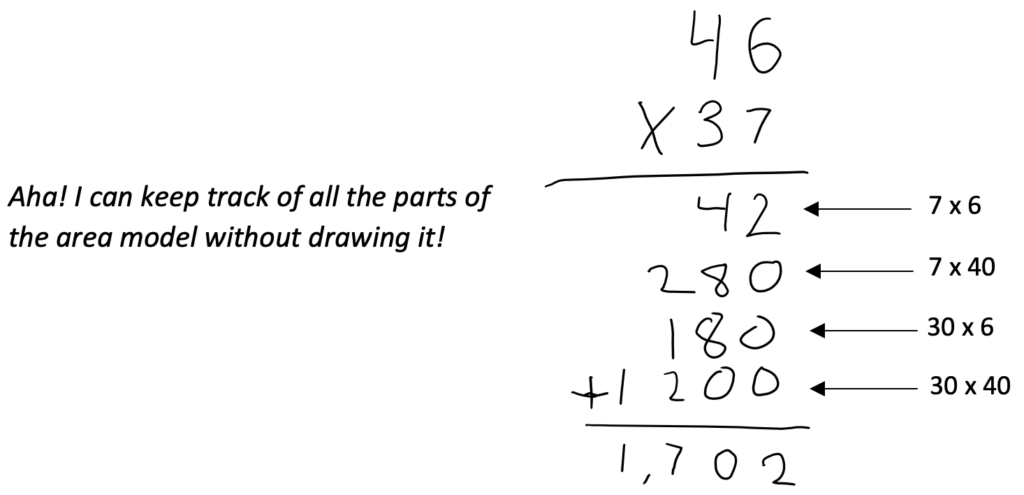
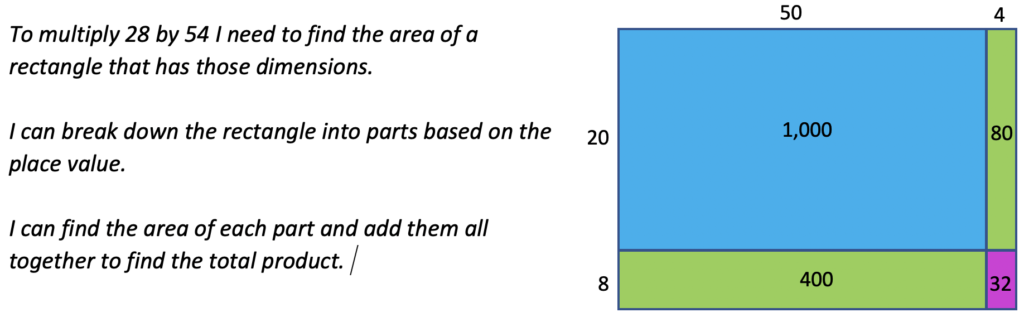
2) The student practices these understandings (not all in one chunk but over time – only a few problems in each practice session) until they become fluent with them. Initially, their thought process might look like this:
After practicing this thought process, it might become shorter – the area model can become a quick sketch.
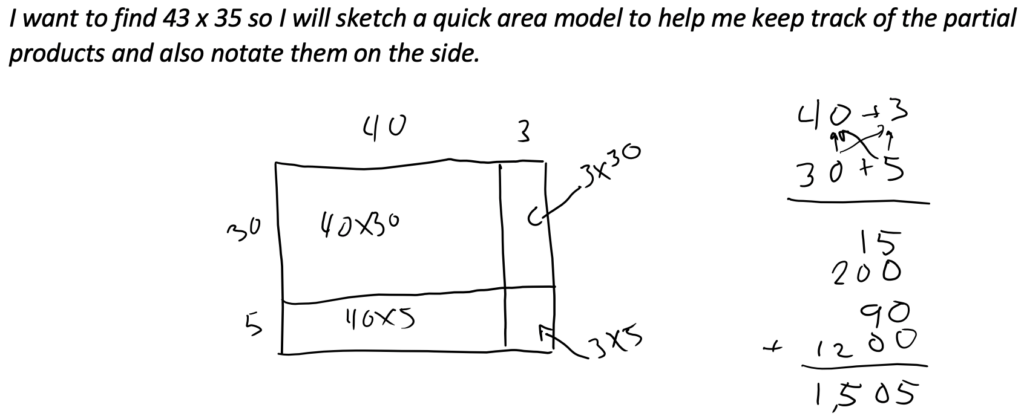
Eventually, the model may live entirely in the student’s head. They may move to an understanding that they need to multiply each part of one number by every part of the other (an understanding that will prove very useful when working with polynomials later!) and find other ways of keeping track of their reasoning. They may even develop several strategies for multiplication that they are comfortable with or the ability to think flexibly enough to generate new strategies on the fly. (There are many ways to multiply two-digit numbers. As students practice their reasoning, they may deepen their understanding so they can think more flexibly about the task overall.)
Practicing reasoning turns the brief Aha! moments of conceptual understanding in the classroom into well-worn neural pathways. Fluency gained in this way means students no longer have to struggle to remember or figure out a strategy each time. They become comfortable in their understanding of the problem. They become confident in their ability to apply multiple strategies. They easily check for reasonableness in their answers. The time spent practicing may be comparable to the time one might spend trying to memorize a procedure, but the results are so much richer.
Even with this kind of practice, you can lose your fluency if you don’t keep using it. The difference is that fluency that was gained through understanding can be regained without starting over from zero. Revisit the conceptual understanding and the fluency will return. (It’s like getting on a bike after a long break… you might wobble at first, but you’ll find your way back to that natural feel quicker than you think!)

Aren Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
