Blog

One Right Answer? One Right Way?

by Sarah Lonberg-Lew

Does every math question have a single right answer? Many people would say yes. In fact, that’s one thing that I’ve heard people say that they love about math. There’s no ambiguity. It’s not a matter of opinion. The answer to 2 + 2 is 4 and that’s the end of the story. It’s clean and clear.

BUT (I hear you cry), what about on the test? On the test there is only one right answer, and it is important that students get it right! It’s true. On the test, and in many other places, there is only one right answer, and it is important to get it right. So, does that mean that math isn’t a flexible and creative subject? After all, if the answer to 2 + 2 is 4, it doesn’t matter how I feel about that. My feelings don’t change the answer.

But suppose I ask you how you know that 2 + 2 = 4?

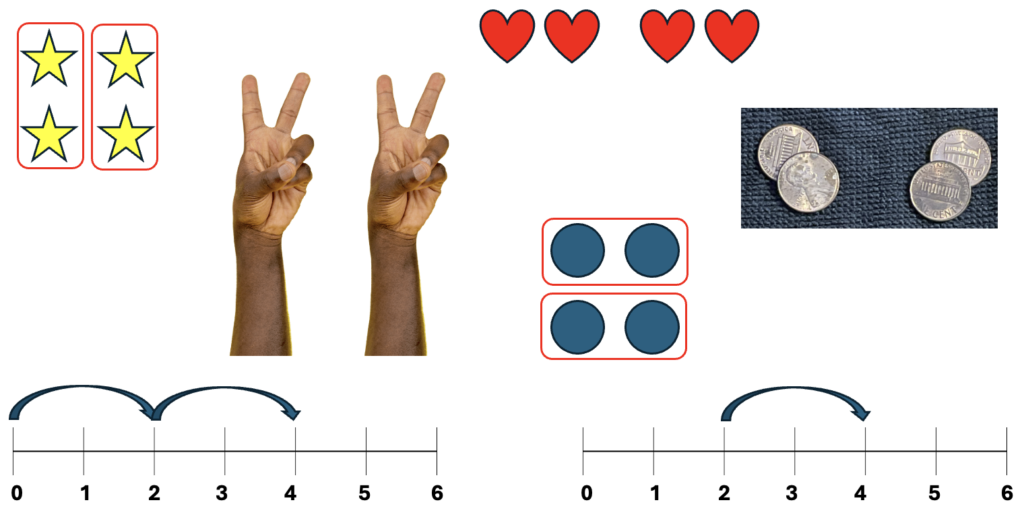
What happened in your brain? Did you hold up two fingers on each hand and then count to see that there were four all together? Did you picture starting at 2 on a number line and then taking two steps forward to land at 4? Or maybe you pictured starting at 0 and taking 2 steps and then 2 more steps. Maybe you thought about asking what number you could add to 2 to get to 4. Did you picture two groups of two objects? How were they arranged? Did you think of real objects or abstract representations? Did you actually take out concrete objects? Did you do something else that I haven’t thought of? Each of these pictures shows that 2 + 2 = 4, but they are not the same pictures, and they don’t reflect the same thinking.

When I say that math is flexible and creative, that doesn’t mean I think that you can decide that 2 + 2 = 5 if that’s what makes you happy. I don’t deny that there are some situations where it is vital to get exactly the one right answer. (And there are also many where there really isn’t a single right answer.) But even when there is only one right answer, there isn’t a single right way to get to it, to reason about it, to visualize it, or to investigate it.

What is the value of being able to think about a math question in more than one way when we already know that there is a procedure in the textbook that works every time? Isn’t it simpler if everyone learns to do math the same way? The procedures in textbooks work, but they also reflect a particular way of thinking, a way of thinking that belongs to a long tradition that is firmly grounded in the dominant culture. Those procedures work, but insisting that they are the best or only way to solve problems excludes people who don’t think in that one specific way—and when you consider all the ways there are to think, that is probably a lot of people. And it is more likely to be those people who don’t come from the same cultural tradition that the textbooks came from. When we insist on math being done a particular way, we can squash students’ intuition and connections to their cultural traditions. When we insist on math being done in one particular way, we remove avenues to success—we make it less likely that our students will find a way to the correct answer because our focus is on memorizing THE way instead of capitalizing on our students’ formidable mental resources.

Yes, it is true that there is only one right answer on the test. It is true that many mathematical questions have only one right answer (and many don’t). But that is not the same as there being only one right way. Math is a flexible and creative subject, even when it comes to getting the right answers on a test!

(For more on the connection between equitable teaching and pushing back against “one right way” thinking, see this short video from Berkeley Everett.)

---