Blog

Making Sense of Long Division

by Sarah Lonberg-Lew

I once had a student show me a mnemonic for the steps of long division: Dad, Mom, Sister, Brother, Cat for Divide, Multiply, Subtract, Bring down, Check. This would never have worked for me because I couldn’t remember the order the family members were to be listed in and what kind of pet they had! (Not to mention the added cognitive load for any student whose family doesn’t look like the one in the mnemonic.) To me, it makes sense to use a mnemonic to remember things like the Great Lakes (HOMES) or the planets (My Very Excellent Mother Just Served Us Nine Pizzas—Pluto is still a planet in my heart). These are things that can only be remembered or looked up but can’t be reasoned about. When something is figure-out-able, I prefer to “remember” by understanding.

But is long division figure-out-able? A few years ago, I had a conversation with another teacher about whether some things in math just needed to be memorized. We talked about long division. We both had memorized the steps in school. Neither of us knew why those were the steps to follow. Maybe that was something you just had to memorize.

Since then I have learned and even created many flexible and conceptual ways to think about division. I rarely do long division anymore, but it gnawed at me to have memorized a procedure I couldn’t make sense of. So I sat down one night and worked it out for myself. If you also want to see some light in the obscurity of long division, see if you can figure out why it works… or read the meaning I found in it below.

I started trying to make sense of long division concretely, thinking about a specific division task:

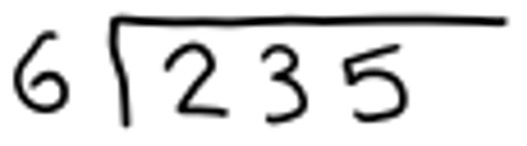
I remember what I am supposed to do here. I know 6 doesn’t go into 2, so I’m supposed to think about how many times it goes into 23. But why? The number I’m dividing is not 23, it is 235.

There are two possible questions I might be trying to answer with this division. One is how many 6s can fit into 235 and the other is what size groups I will get if I split 235 into 6 equal groups. I decided to think about the second approach. I imagined I had 235 objects and I wanted to put them into 6 bins.

To start, I drew a picture of my 235 objects using a place value visualization:

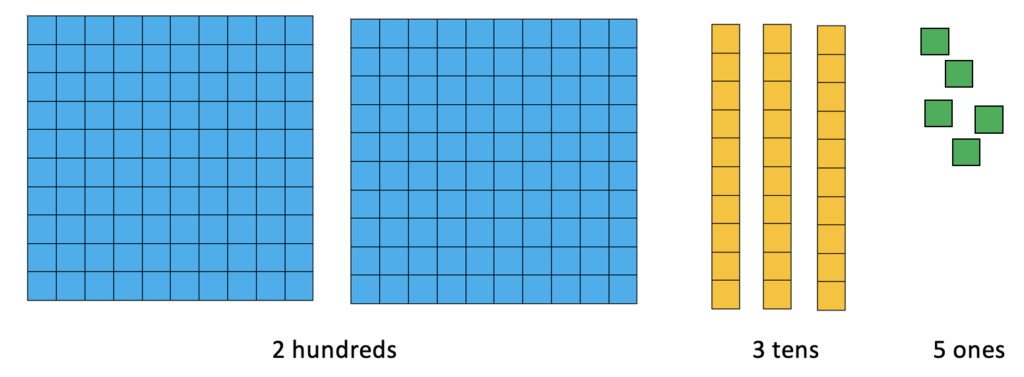
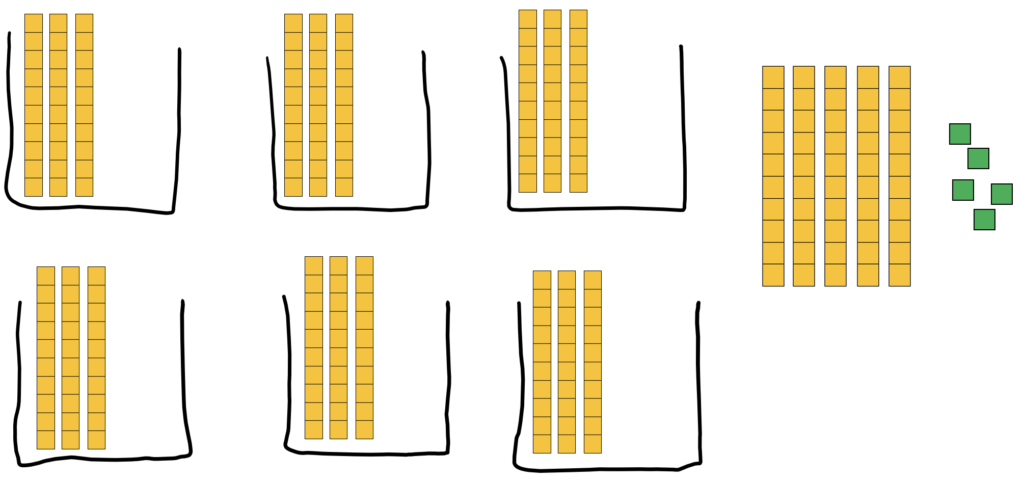
And I drew a picture of my 6 bins:

When I started to split up my 235 objects equally into my 6 bins, I decided to start with the biggest chunks. I immediately saw a problem: I had two hundreds. That wasn’t enough to put even one in each bin, so what could I do with them?

I decided to split up my hundreds into tens so now my 235 objects looked like this:

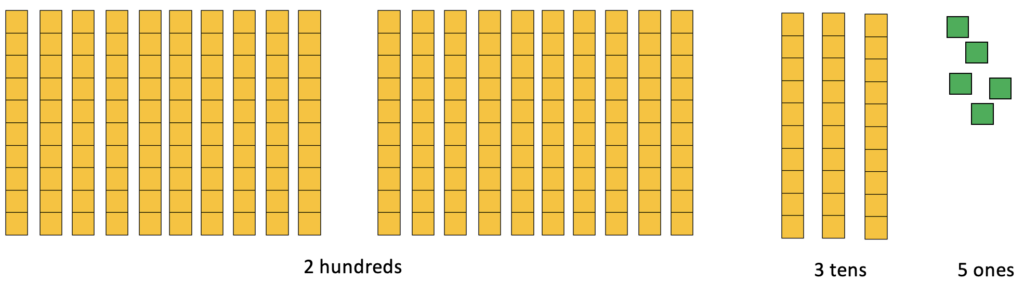
Oh! Now I could see the number 23 in my model! There were 23 tens to be split up into 6 bins. I put as many as I could in each bin until I didn’t have enough left to put one more in each bin:

Using paper and pencil long division, I wrote down the 3 tens as part of the quotient because I knew there would be no more than 3 tens in each bin. Also, I could see that the total number of objects I’d parceled out is 3 tens times 6 (the Multiply step), so it made sense to Subtract that number to see how many objects I had left to distribute. So my long division looked like this:

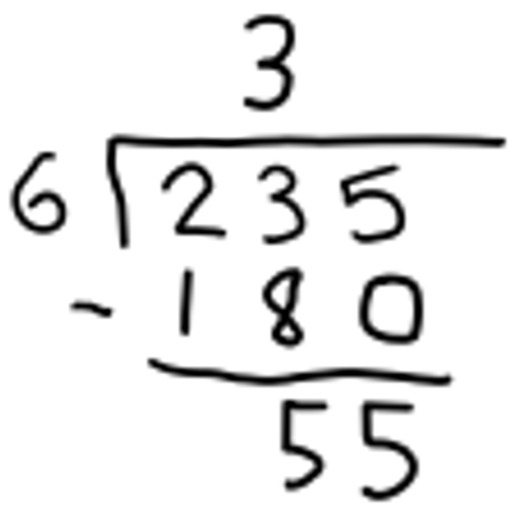
(Actually, this looks a little different from how I was trained to do long division. I was taught to just multiply 6 times 3 and write the 18 below the 23, but from my model, I could see that I was working with 18 tens and 23 tens, so it made sense to subtract 180 from 235 instead subtracting 18 from 23 and then “Bringing down” the 5. This way, the 5 is brought down naturally as part of the subtraction. And I could see why I subtracted—I was taking away the objects that had already been put into bins so I could see how many were left to distribute.)

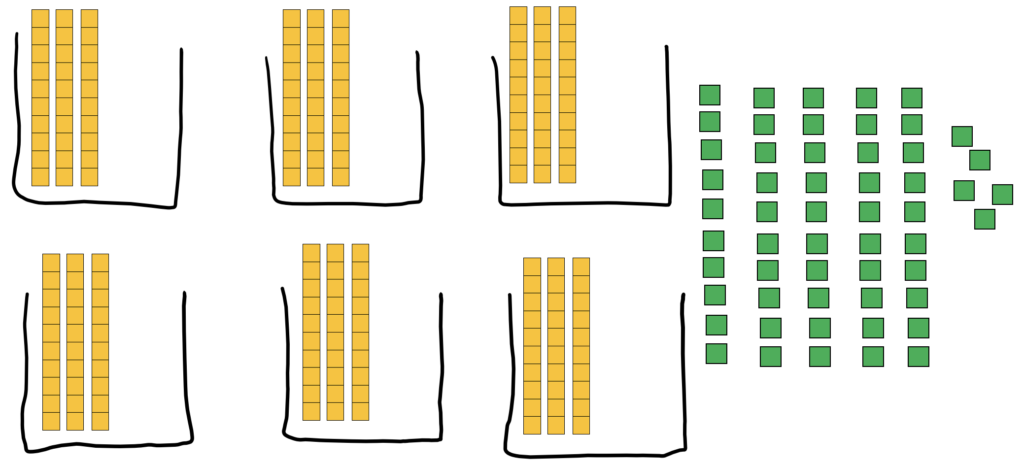
So, I had handed out 18 tens into the bins and there were 5 tens left over because 5 wasn’t enough to put one more in each bin. Also there were still the 5 ones that I hadn’t dealt with. All the objects were still in the picture, but just rearranged. (In my long division above, I could see these tens and ones in the number 55 at the bottom.)

Since I didn’t have enough tens left to put a whole ten in each bin, I split up my tens into ones:

Now I could start splitting up the leftover ones into my 6 bins. There were 55 ones to split up, so I had enough to put 9 in each bin:

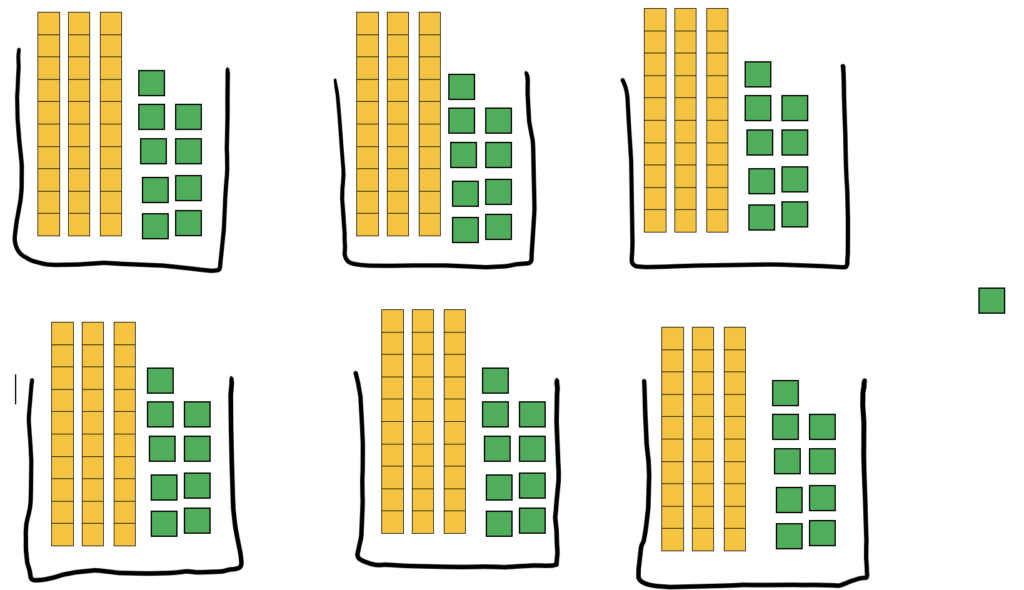
(In the long division, this is like going back to the Divide step because I’m splitting up objects into groups. In the last Divide step, I was splitting up the tens. Next, I split up the ones.)

I could now see in my model that my quotient would have 9 ones because there were 9 ones in each bin. I could also see that there would be a single 1 left over after Subtracting the 54 (9 Multiplied by 6) I’d put in the bins from the number that was still to be divided. My long division now looked like this:

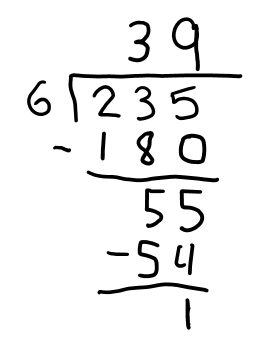
From there, I had to decide what I wanted to do with that leftover one. I could write the quotient as 39 R 1, I could consider what fraction of that piece would go in each bin, or I could think about continuing to split up the leftover pieces into smaller and smaller pieces and parceling out those pieces until I was satisfied. I’ll leave it up to you to take it further if you choose.

Even though I now understand why long division works, it’s not my preferred method of teaching or doing division. This procedure is a way of keeping track of a certain way of reasoning about division. There’s nothing wrong with that way of reasoning, but it isn’t the only way. For both teaching and doing division, I want to have the flexibility to visualize and make sense of the situation, estimate, and reason about it in a way that makes sense to me—choosing how to approach it based on the numbers involved and the context. For example, if I had been dividing 235 by 57 instead of by 6, I might decide not to think about 57 bins (that’s a lot of bins!) and instead to think about how many groups of 57 fit into 235. Would the long division procedure also make sense as a way of keeping track of that way of thinking? I’ll leave that particular mathematical adventure to you!

---