How I Learned to Stop Worrying and Love Percents
by Sarah Lonberg-Lew
When I was about 8 years old, I went on a “date” with my best friend. My mother dropped us off at a restaurant with some money and we ordered burgers, fries, and ice cream sundaes, just like a couple of grown-ups. Everything went fine until we got the bill and realized we were supposed to leave a tip and neither of us had learned how to do percents! Luckily, the kind waitress helped us work it out. I remember her explaining what she was doing, but I don’t remember understanding it. What I did understand about percents at the time was that they were hard and complicated and I’d probably learn about them someday when I was all grown up like that waitress (who was probably a high-school student).
When I told my mother about it, she told me something that changed my relationship with percents forever. She told me that 1% was the same as one hundredth. In other words, if I broke a number into 100 pieces, each of those pieces was 1% of that number. It was as if she had given me the keys to the kingdom. With that one bit of information, I felt I could figure out anything I ever needed to know about percents. Figuring out a 15% tip? Just divide the bill by 100 to find 1%, and then multiply it by 15 to get 15%.
But in school, things got more complicated. I was taught different kinds of percent problems, each requiring a different procedure. Depending on which kind of percent problem I was doing I learned to convert the percent to a decimal and then multiply by the whole, or sometimes divide the part by the percent, or other times divide the part by the whole! I also learned how to translate percent problems into algebraic equations and solve them using the rules of algebra. I dutifully memorized all the procedures and became quite adept at useful things like figuring out what the whole was if 17.3 was 83% of it. I got so good at those procedures that, for a long time, I forgot that I already had the keys to the kingdom.
When I first became a teacher and taught students how to solve percent problems, I taught them the procedures I had memorized. My students had the same initial ideas about percents that I had held – that they were hard and complicated and only people who were really good at math could figure them out without a tip-card or an app. I’ve found that being able to calculate with percents is something that most adult students really want to learn because it does come up so often in their lives. Not being able to make sense of percents can feel frustrating or embarrassing.
I realized that teaching students three different procedures for three different types of problems only strengthened their mistaken belief that understanding percents was too difficult for the average person. It was when I began to learn about teaching percent concepts with benchmark fractions that I started to find my way back to a place of understanding. Students didn’t have to wait until they were ready to work at a sixth grade level before they could start reasoning with percents. Any student who could make sense of ½ could also make sense of 50%. Likewise, students who could reason about ¼ and ¾ could reason about 25% or 75%.
It turns out that the key concept my mom had shared – knowing that 1% was equal to 1/100 – was only one of several that helped turn percent calculations from an exercise in applying memorized procedures to one in reasoning. I thought of 1% as my friend. If I could find my way to 1%, I could find my way anywhere! Since then, I’ve made many friends in the realm of percents. 50%, who also sometimes goes by the names ½ or 0.5, is useful for quick calculations and estimations. Her siblings, 25% and 75% help me achieve greater precision without a lot of mental effort. And there’s an extended family that I have gotten to know through expanding my set of benchmarks (a process that takes time). Once I got friendly with multiples of 10% and 5%, I was prepared to estimate my way through any percent scenario. And if I need a precise answer, my first friend 1% is always there for me (as is my calculator when numbers get messy!).
The procedures I learned in school were efficient and accurate, but it required practice and memorization to develop fluency with them. Memorization can be a difficult and unreliable route for many learners, but reasoning is accessible to everyone. It took time for me to get to know the extended family of percent benchmarks that I feel so at home with now, but even with just a few benchmarks, students at any level can begin to approach percents through reasoning.
See It in Pictures
Want to see how my friends help me work out what the whole is if 83% of it is 17.3?
Let’s start with an estimate: 83% is almost the same as four blocks of 20% (and 20% is the same as 1/5 of the whole).
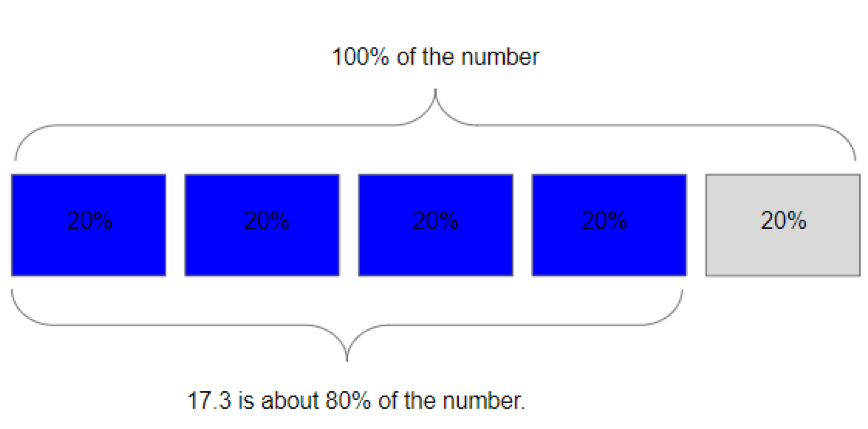
If four blocks of 20% put together is 17.3, then I can divide 17.3 by four to find the size of one block of 20%. 17.3 divided by four is close to 4. So 20% (one block) of the number I’m trying to figure out is close to 4.
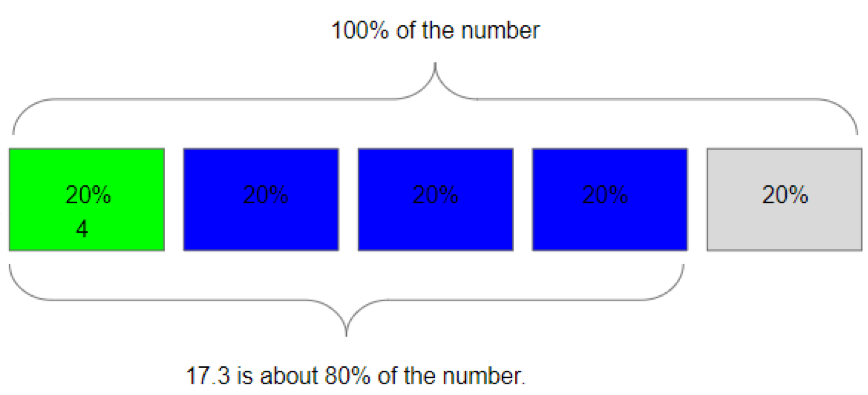
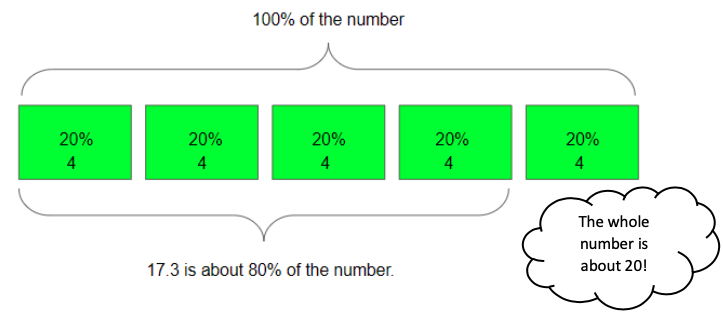
That means if I multiply 4 times five (total blocks in the whole), I can figure out about how much 100% of the whole would be.
Want to be more precise? Time to call on my friend 1%! I know that 83% is 83 blocks of 1%, so if I divide 17.3 into 83 pieces, each one of those will be 1% of the whole. This is calculator time. 17.3 divided by 83 gives me 0.2084 (rounded).
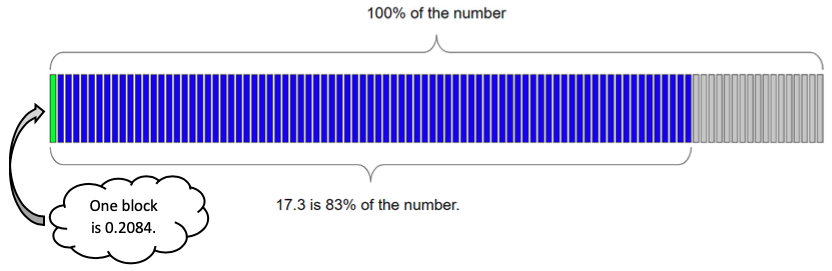
That’s 1%, so 100% will be 100 times that or 20.84.
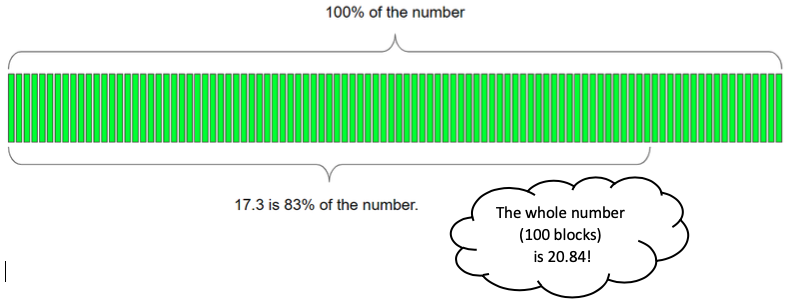
(I’d better just check to make sure that’s reasonable… 83% of a number is most of that number, and 17.3 is most of 20.84. Looks reasonable to me!)

Sarah Lonberg-Lew has been teaching and tutoring math in one form or another since college. She has worked with students ranging in age from 7 to 70, but currently focuses on adult basic education and high school equivalency. She teaches in an adult education program in Gloucester, MA. Sarah’s work with the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center at TERC includes developing and facilitating trainings and assisting programs with curriculum development. She is the treasurer for the Adult Numeracy Network.
