Finite Geometry or, How I Learned about a Math Topic I’d Never Heard of Before
by Mark Trushkowsky
Last month I wrote a blog about Dr. Minerva Cordero and the sense of connection and belonging I felt when I learned about a mathematician who shares an aspect of my identity. I wanted to share another aspect of my journey and write about Dr. Cordero’s work in mathematics.
My wife used to work in exhibit design, designing informational spaces like museums or aquariums. They used a framework called “the 5 Ss” “to consider the different ways people might move through the space. Streakers move through quickly, only catching the headlines and large and simple visuals. Strollers move slower, and take in a little more, but aren’t really stopping. Students want to learn and will stop and maybe even move forwards and backwards as they make sense of things. Scholars are already experts in the content who are there out of passion and curiosity. The final S is for Selfie—the showstopper moment, usually something visual, that makes everyone want to stop and take a photo.

When researching mathematicians and their biographies, I tend to be a bit of a streaker when it comes to the actual work that they do. I usually focus more on their compelling stories and less on their work in mathematics, which is almost always in a field of mathematics that I’ve never heard of. Case in point, Dr. Cordero’s area of expertise and exploration is in something called finite geometry.
This time I decided to take inspiration as an invitation to poke around something.
I take heart in the fact that math at the level we are talking about is almost always about questions and the unknown. Professional and academic mathematicians have studied a lot more math than me, but they are looking at and for things they don’t understand, which means they make mistakes and get it wrong more than they get it right. We are all pushing and stretching the definitions of what it means to do math, even though we are doing it in very different spheres and at very different levels.
It reminds me of the WIRED web series, 5 Levels, where they get experts to explain different concepts—things like Memory, Black Holes, Fractals, Infinity, Time—at five different levels of complexity. The levels are child, teenager, college student studying the topic, graduate student (or professional), and another expert in the field. The central question is whether they can explain the concept and be understood at every level.
With all of this in mind, I set out to learn something about finite geometry, and I’d like to share what I’ve learned so far, both about finite geometry and how I tried to learn something in math that I had never heard of before.
From Dr. Cordero herself, I learned that finite geometry is at the intersection of algebra, geometry, and combinatorics (which I think of as the math of counting and arranging). Most of the questions driving her work are around how to safely encode and decode information. She talks about how much data it takes to store just one picture. If we don’t design a way to use very little space in the computer, we won’t be able to store many pictures. This has applications in everything from animated movies to MRI machines and CAT scans. In her words, “My specific area of mathematics has to do with all this type of saving information and transmitting information in the safest and most efficient way.”
I searched the internet and was a bit of a streaker through lots of pages that were hard to make sense of. At one point, I even asked ChatGPT how it would explain finite geometry to a 6th grader. Like many of the responses I get from ChatGPT, it was vague and left me with more questions than answers BUT it has clearly learned that using the language of play is the way to my heart.
Here is its response:
Imagine you’re playing with a piece of paper with some dots on it. You know how in regular geometry, you can draw lines that go on forever and ever? Well, in finite geometry, we play a bit of a different game. In finite geometry, we pretend our paper has edges, like a small map of a made-up world. That means there are only a certain number of dots on our paper, and we can only draw lines that connect these dots. It’s like playing on a small playground instead of a gigantic field. So, finite geometry is all about exploring shapes, lines, and patterns on this limited paper. Sometimes, lines might look like they’re curving or bending because they have to stay inside the edges of our paper. It’s like drawing on a treasure map where you have to follow the clues and stay inside the map’s borders. In a nutshell, finite geometry is like a fun adventure on a small piece of paper, where we discover all sorts of interesting things about shapes and lines within our little world. It’s a bit like solving puzzles and exploring a new kind of math playground!
I didn’t feel any closer to understanding what finite geometry is, but that last sentence made me change up my approach. Instead of searching for definitions of finite geometry, I started searching for core puzzles and problems in finite geometry. I also started doing image searches for “finite geometry.”
And that’s when I went from a Stroller to a Student.
One puzzle I found is called The Diamond 16 Puzzle.
It involves changing the pair of patterns (below left) to match other pairs of patterns (below right).

In addition to the website linked above, I also liked working on this puzzle with these black & white virtual Truchet tiles.
Another helpful step for exploring an unknown field of mathematics is to do an image search.
When I searched images of finite geometry, I found all of these interesting diagrams of dots and lines, like this one on the right, called the Fano plane.
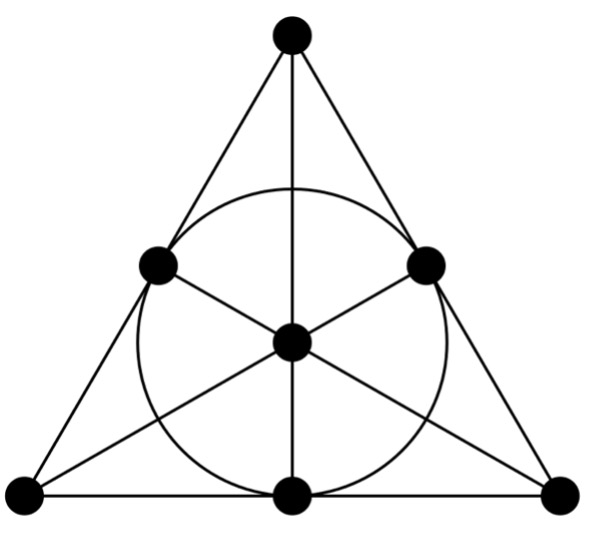
I also found a video from Professor Heather Pierce that was really helpful, but there are spoilers so you will find the link to her video at the end of this post. In the video, she describes finite geometry as constructing different geometric figures that satisfy different conditions (a certain number of points, lines, intersections, etc.). For example, the Fano plane is based on the following 5 conditions:
- There exists at least one line.
- Every line has exactly three points on it.
- Not all points are on the same line.
- Every point has to connect to every other point.
- Every two lines have to share at least one point.
So how does that work?

Here’s a video talking through the above.
What I understand about finite geometry could be represented by water in a thimble. I know so little and what I think I know slips through my fingers as quickly as it comes. But one thing I appreciate is how aspects of it can be conveyed as simple (accessible) and challenging puzzles.
Want to try one?
Draw a model that has nine points and twelve lines, such that each line has exactly 3 points and each point is the intersection of exactly 4 lines.
Have some fun and play around with it for a bit. When you are ready to see an answer (I’m not sure if it’s the only answer), you can find one here: Hesse configuration
Below is Professor Pierce’s video on Finite Geometry, but don’t watch it until you’ve played around with this final puzzle, since it’s one of the models she draws. Enjoy!

Mark Trushkowsky is a professional developer, curriculum writer, and math teacher at the CUNY Adult Literacy and High School Equivalency Program. He is co-author of the CUNY Fast Track Math GRASP Packets. He is also a facilitator and developer for the SABES Mathematics and Adult Numeracy Curriculum & Instruction PD Center.
